Maxwellove jednadžbe

Elektromagnetizam

Ključne stavke

Elektricitet • Magnetizam

Elektrostatika

Električni naboj • Coulombov zakon • Električno polje • Električni fluks • Gaussov zakon • Električni potencijal • Elektrostatična indukcija • Električni dipolni moment

Magnetostatika

Ampèreov zakon • Električna struja • Magnetno polje • Magnetni fluks • Biot–Savartov zakon • Magnetni dipolni moment • Gaussov zakon za magnetizam

Elektrodinamika

Vakuum • Lorentzova sila • EMS • Elektromagnetska indukcija • Faradayjev zakon • Lenzov zakon • Struja pomaka • Maxwellove jednačine • EM polje • Elektromagnetna radijacija • Liénard-Wiechertov potencijal • Maxwellov tenzor • Vrtložne struje

Električna mreža

Električna provodljivost • Električni otpor • Kapacitivnost • Induktivnost • Impedanca • Resonantne šupljine • Talasovod

Kovarijantna formulacija

Elektromagnetni tenzor • EM tenzor napon-energija • Četiri-tok • Elektromagnetni četiri-potencijal

Naučnici Ampère • Coulomb • Faraday • Heaviside • Henry • Hertz • Lorentz • Maxwell • Tesla • Weber · Ostali

Ova kutijica: pogledaj • razgovor • uredi

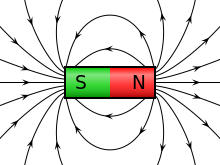
Maxwellove jednadžbe (po J. C. Maxwellu) čine osnovu klasične elektrodinamike i izražavaju povezanost električnog i magnetskoga polja. Maksvelove jednačine obuhvataju ranije poznate zakone, koje je Maxwell objedinio u skladu sa jednadžbom kontinuiteta:

• Gaussov zakon električnoga polja,
• Gaussov zakon magnetskoga polja,
• Faradejev zakon elektromagnetne indukcije,
• Amperov zakon magnetnog polja.

Po Maksvelovim jednačinama, promjene u električnom polju uzrokuju promjene u magnetskome polju, i obrnuto, i dovoljno je u nekom trenutku poznavati električno i magnetsko polje kako bi se mogle odrediti promjene polja u budućnosti. ^[1]

Maxwellove jednadžbe su temelj klasične elektrodinamike i teorijske elektrotehnike. Neki put se ovom skupu pridruži i Lorencova jednačina.

Zakoni

Gaussov zakon električnoga polja

Glavni članak: Gaussov zakon električnoga polja

Gaussov zakon govori da je električni naboj izvor električnog polja. Ukupni električni tok kroz zatvorenu površinu proporcionalan je količini električnog naboja koji se nalazi unutar zapremine te površine. Ako unutar te zatvorene površine nema električnog naboja, ukupni električni tok kroz tu zatvorenu površinu je nula. To ne znači da u toj zapremini uopšte nema električnog polja, već samo da ukupni tok iščezava. Dakle, ako nema električnog naboja u posmatranoj zapremini, koliko silnica električnog polja ulazi kroz površinu koja opisuje zapreminu, toliko ih izlazi iz te zatvorene površine.

Gaussov zakon magnetskoga polja

Glavni članak: Gaussov zakon magnetskoga polja

Gaussov zakon magnetskoga polja je sličan prethodnom (u situaciji u kojoj ne postoji naboj), ali opisuje magnetno polje. Ovaj zakon izriče činjenicu da magnetskih monopola u prirodi nema. Postoje samo dipoli a jedini izvor magnetnog polja je električna struja i promenljivo električno polje. U svakoj tački prostora, količina silnica magnetnog polja koja ulazi u tu tačku jednaka je količini silnica koje izlaze iz te tačke. Stoga ukupni magnetni tok kroz zatvorenu površinu uvek iščezava.

Faradejev zakon indukcije

Glavni članak: Faradejev zakon indukcije

Faradejev zakon indukcije pokazuje da je promenljivo (nestatičko) magnetno polje uzrok nastanka električnog polja - fenomen poznat kao elektromagnetna indukcija. Zakon elektromagnetske indukcije jedan od osnovnih i najvažnijih zakona elektrotehnike. To je osnovni princip rada transformatora, induktora i mnogih vrsta električnih motora, generatora i solenoida.^[2][3]

Amperov zakon magnetnog polja

Glavni članak: Amperov zakon magnetnog polja

Amperov zakon objašnjava nastanak magnetnog polja oko zatvorenog električnog kola, povezujući električne i magnetske pojave.^[4] Električna struja koja teče kroz provodnik stvara magnetsko razmjerno jačini struje i dužini provodnika, a obrnuto razmjerno udaljenosti od provodnika.^[5] Smjer magnetskog polja okomit je na struju. Ako kroz dva usporedna provodnika struja teče u istom smjeru, oni se privlače; u protivnom odbijaju.^[6]

Jednačine

Maksvelove se jednačine mogu prikazati u diferencijalnom i integralnom obliku. Ekvivalencija između ovih oblika zasniva se na Stoksovoj i Gaus-Ostrogradski teoremima. Takođe postoji i četvorodimenzionalni oblik koji se koristi u teoriji relativnosti i kvantnoj elektrodinamici.

Naziv	Integralna jednačina	Diferencijalna jednačina
Gaussov zakon električnoga polja	${\displaystyle {\scriptstyle \partial \Omega }}$${\displaystyle \mathbf {E} \cdot \mathrm {d} \mathbf {S} ={\frac {1}{\varepsilon _{0}}}\iiint _{\Omega }\rho \,\mathrm {d} V}$	${\displaystyle \nabla \cdot \mathbf {E} ={\frac {\rho }{\varepsilon _{0}}}}$
Gaussov zakon magnetskoga polja	${\displaystyle {\scriptstyle \partial \Omega }}$${\displaystyle \mathbf {B} \cdot \mathrm {d} \mathbf {S} =0}$	${\displaystyle \nabla \cdot \mathbf {B} =0}$
Faradayev zakon indukcije	${\displaystyle \oint _{\partial \Sigma }\mathbf {E} \cdot \mathrm {d} {\boldsymbol {l}}=-{\frac {\mathrm {d} }{\mathrm {d} t}}\iint _{\Sigma }\mathbf {B} \cdot \mathrm {d} \mathbf {S} }$	${\displaystyle \nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}}$
Ampèreov zakon magnetnog polja	${\displaystyle {\begin{aligned}\oint _{\partial \Sigma }&\mathbf {B} \cdot \mathrm {d} {\boldsymbol {l}}=\mu _{0}\left(\iint _{\Sigma }\mathbf {J} \cdot \mathrm {d} \mathbf {S} +\varepsilon _{0}{\frac {\mathrm {d} }{\mathrm {d} t}}\iint _{\Sigma }\mathbf {E} \cdot \mathrm {d} \mathbf {S} \right)\\\end{aligned}}}$	${\displaystyle \nabla \times \mathbf {B} =\mu _{0}\left(\mathbf {J} +\varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}\right)}$

U Maksvelovim jednačinama implicitno se pretpostavlja da vredi jednačina kontinuiteta (zapravo zakon očuvanja naboja):

${\displaystyle {\partial {\rho } \over \partial t}+\nabla \cdot \mathbf {J} =0}$

Za potpuni opis elektromagnetskih pojava nužna je i Lorencova jednačina, kako bi se iz polja mogla odrediti sila:

${\displaystyle \mathbf {F} =q\cdot (\mathbf {E} +\mathbf {v} \times \mathbf {B} )}$

Simboli i jedinice

U gornjim jednačinama korišteni su simboli SI mernih jedinica :

Simbol	Značenje	SI jedinice mere
${\displaystyle \mathbf {E} }$	električno polje	volt po metru ili, njutn po kulonu
${\displaystyle \mathbf {H} }$	magnetsko polje	amper po metru
${\displaystyle \mathbf {D} }$	električna indukcija	kulon po kvadratnom metru
${\displaystyle \mathbf {B} }$	magnetska indukcija	tesla, ili, veber po kvadratnom metru
${\displaystyle \ \rho \ }$	gustina naelektrisanja	kulon po kubnom metru
${\displaystyle \mathbf {J} }$	gustina električne struje	amper po kvadratnom metru
${\displaystyle \mathrm {d} \mathbf {A} }$	odsečak površine po kojoj se integrali	kvadratni metar
${\displaystyle \mathrm {d} V\ }$	deo prostora obuhvaćenog zatvorenom površinom S	kubni metar
${\displaystyle \mathrm {d} \mathbf {l} }$	deo konture koja okružuje površinu S	metar
${\displaystyle \nabla \cdot }$	operator divergencije	po metru
${\displaystyle \nabla \times }$	rotor operator	po metru

${\displaystyle \epsilon _{0}\ }$ - dielektrična konstanta vakuuma (permitivnost),

${\displaystyle \mu _{0}}$ - permeabilnost vakuuma, a jednaka je:

${\displaystyle \mu _{0}={1 \over {\varepsilon _{0}\cdot c^{2}}}}$

gde je ${\displaystyle c\ }$ brzina svetlosti.

Makroskopska formulacija

Maksvelove jednačine opisuju ponašanje električnog i magnetnog polja svugde u prostoru, ako su poznati svi izvori, to jest naboji i struje. U opisu makroskopskih objekata takav pristup nije moguć iz dva razloga. Prvo, broj naelektrisanih čestica u atomima i nuklearnim jezgrama vrlo je velik. Drugi je razlog da sa makroskopske tačke gledanja, svi detalji u ponašanju polja i naboja na atomskim i molekularnim dimenzijama nisu relevantni. Ono što je bitno, to je prosečna vrednost polja i izvora u zapremini koja je velika u poređenju sa jednim atomom ili molekulom. Ovakve prosečne vrednosti nazivaju se makroskopska polja i makroskopski izvori. U ovom slučaju Maksvelove jednačine poprimaju oblik:

${\displaystyle \nabla \cdot \mathbf {D} ={\rho _{slob.}}}$

${\displaystyle \nabla \cdot \mathbf {B} =0}$

${\displaystyle \nabla \times \mathbf {E} +{\frac {\partial \mathbf {B} }{\partial t}}=0}$

${\displaystyle \nabla \times \mathbf {H} -{\frac {\partial \mathbf {D} }{\partial t}}={\mathbf {J} _{slob.}}}$

gde je:

${\displaystyle \mathbf {D} \ }$ - polje električnog pomaka,

${\displaystyle \mathbf {H} \ }$ - magnetizirajuće polje,

${\displaystyle {\rho _{slob.}}\ }$ - gustina slobodnog električnog naboja (ukupna gustina električnog naboja minus gustina vezanih električnih naboja),

${\displaystyle {\mathbf {J} _{slob.}}\ }$ - gustina slobodne električne struje (ukupna gustina električne struje minus gustina vezanih električnih struja).

Veličine ${\displaystyle \mathbf {D} \ }$ i ${\displaystyle \mathbf {H} \ }$ nije jednostavno odrediti, jer je u njima sadržana celokupna složenost interakcije polja i sredstva (medija, to jest materijala u kojem se polje nalazi). Moguće je da ove veličine zavise od prethodnog stanja sredstva (histerezis), takođe je moguće da su nelinearne i prostorno anizotropne. Ove jednačine za polja u sredstvu nisu toliko univerzalne kao početno navedene jednadžbe. Ipak, J. K. Maksvel ih je na sličan način prvobitno formulisao. Veze između ${\displaystyle \mathbf {E} \ }$ i ${\displaystyle \mathbf {D} \ }$ te između ${\displaystyle \mathbf {B} \ }$ i ${\displaystyle \mathbf {H} \ }$ zovu se konstitutivne relacije.

U najjednostavnijem slučaju pretpostavlja se, da su električna i magnetska svojstva sredstva homogena i izotropna, te da se polja ne menjaju intenzivno u vremenu. U stvarnosti to vredi za dielektrične i paramagnetske materijale. Tada spoljašnje električno polje stvara polarizaciju ${\displaystyle \mathbf {P} \ }$, koja je linearno proporcionalna električnom polju, dok magnetno polje stvara magnetizaciju ${\displaystyle \mathbf {M} \ }$ proporcionalnu magnetnom polju, te vredi:

${\displaystyle \mathbf {P} \ =\chi _{e}\cdot \epsilon _{0}\cdot \mathbf {E} }$

${\displaystyle \mathbf {M} \ =\chi _{m}\cdot \mathbf {H} }$

Tada je:

${\displaystyle \mathbf {D} \ =\epsilon _{0}\cdot \mathbf {E} +\mathbf {P} =\epsilon _{0}\cdot (1+\chi _{e})\cdot \mathbf {E} =\epsilon \cdot \mathbf {E} }$

${\displaystyle \mathbf {B} =\mu _{0}\cdot (\mathbf {H} +\mathbf {M} )=\mu _{0}\cdot (1+\chi _{m})\cdot \mathbf {H} =\mu \cdot \mathbf {H} }$

Izvori

Vidi još

• Lorencova sila
• Bio-Savarov zakon
• Kulonov zakon

Spoljašnje veze

• Maksvelove jednačine elektromagnetnog polja