Număr complex

În matematică, numerele complexe sunt numere introduse ca soluții ale ecuațiilor de forma ${\displaystyle x^{2}+p=0,}$ cu p număr real strict pozitiv.

Formal, corpul numerelor complexe, notat cu ${\displaystyle \mathbb {C} }$, este mulțimea tuturor perechilor ordonate de numere reale (a, b), înzestrată cu operațiile de adunare și înmulțire definite mai jos:

${\displaystyle (a,b)+(c,d)=(a+c,b+d)\,,}$

${\displaystyle (a,b)\cdot (c,d)=(ac-bd,bc+ad)\,.}$

Elementul neutru al operației de adunare este ${\displaystyle (0,0)}$ iar elementul neutru al operației de înmulțire este ${\displaystyle (1,0).}$

Deoarece ${\displaystyle (a,0)+(c,0)=(a+c,0)}$ și ${\displaystyle (a,0)(c,0)=(ac,0)}$, mulțimea numerelor reale poate fi privită ca subcorp a lui ${\displaystyle \mathbb {C} }$, identificând numărul real ${\displaystyle a}$ cu ${\displaystyle (a,0).}$

Numărul complex ${\displaystyle i=(0,1)}$ are proprietatea ${\displaystyle (0,1)\cdot (0,1)=(-1,0),}$ adică ${\displaystyle i^{2}=-1.}$ Fiindcă niciun număr real nu are această proprietate, numărul i a fost denumit „unitatea imaginară” de René Descartes, iar de aici vine notația i. În present, „numerele imaginare” se referă la numere complexe de forma ${\displaystyle (0,x),}$ adică xi cu x număr real.

Există o similaritate între operația de adunare a numerelor complexe și adunarea vectorilor. Numerele complexe permit obținerea unor valori pentru funcțiile sinus, cosinus prin rezolvarea prin 2 procedee (algebric și trigonometric) a unei ecuații binome implicând rădăcini ale unității.

Istoric

Așa cum numerele iraționale apăruseră din necesitatea de a descrie soluții ale ecuațiilor de forma ${\displaystyle \ x^{2}-q=0,}$ unde q nu este un pătrat perfect, numerele complexe au fost introduse ca soluții ale ecuațiilor de forma ${\displaystyle x^{2}+p=0,}$ cu p număr real strict pozitiv.

Primul matematician care menționează sumar radicali de ordinul II din numere negative exprimate ca diferență de numere intregi pozitive e Heron din Alexandria la un calcul legat de o mărime geometrică pentru trunchiul de con.

Următorul matematician care descoperă prezența radicalilor din numere negative (la studiul ecuației de gradul al treilea) e Girolamo Cardano in 1545. Tratatul din 1572 al lui Rafael Bombelli face un studiu al regulilor operațiilor cu numere complexe. Acest studiu e continuat în secolul următor de René Descartes și John Wallis, ulterior de Abraham de Moivre și Roger Cotes care stabilesc conexiunea dintre numere complexe și trigonometrie. Cotes in 1715 ajunge la a deduce formula lui Euler sub formă logaritmică. Logaritmii numerelor negative ca numere complexe sunt analizați de Leonhard Euler.

Ulterior se extinde la scară extinsă printre matematicieni acceptarea reprezentării geometrice prin planul complex cu Caspar Wessel, Jean Robert Argand și Carl Friedrich Gauss (în memoriul său din 1932).

Forma algebrică

Ținând cont de cele de mai sus, orice număr complex z corespunde la o singură pereche ordonată ${\displaystyle (a,b),}$ unde a și b sunt numere reale, și poate fi scris

${\displaystyle z=(a,b)=(a,0)+(b,0)(0,1)=a+bi.}$

Această scriere ${\displaystyle z=a+bi}$ este numită forma algebrică a numărului z. Spre exemplu:

• ${\displaystyle (0,0)=0}$ și ${\displaystyle \ (1,0)=1.}$
• ${\displaystyle (0,1)=i}$ este numit unitatea imaginară sau, mai simplu, „numărul i”. Are proprietatea ${\displaystyle i^{2}=-1.}$

Pentru un număr complex ${\displaystyle z=a+bi,}$ ${\displaystyle a}$ se numește partea reală a lui ${\displaystyle z}$ și se notează ${\displaystyle a=\mathrm {Re} (z),}$ iar ${\displaystyle b}$ se numește partea imaginară a lui ${\displaystyle z}$ și se notează ${\displaystyle b=\mathrm {Im} (z).}$ Un număr complex cu partea reală nulă (deci de forma ${\displaystyle z=bi}$) se mai numește „număr imaginar”.

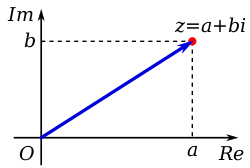
Reprezentarea geometrică a numerelor complexe

Așa cum unui număr real îi se poate asocia un punct de pe o dreaptă, tot astfel, unui număr complex îi se poate asocia un punct aflat într-un plan denumit planul complex. Numărului complex ${\displaystyle z=a+bi}$ i se asociază punctul M(a, b) situat pe un cerc de rază egală ca lungime cu modulul r numărului complex. Această asociere stă la baza diagramelor Argand. Raza unui cerc dusă din originea sistemului de coordonate până la punctul M este un vector euclidian de poziție al punctului respectiv.

Reprezentarea grafică pentru numere complexe a fost studiată începând cu John Wallis.

Planul complex cartezian

Reprezentarea numerelor complexe în planul complex se poate face prin coordonatele carteziene constituite de axa reală orizontală (abscisa) Ox și axa imaginară verticală (ordonata) Oy.

Planul complex în coordonate polare

Folosirea unui sistem de raportare prin coordonate polare în plan permite situarea punctului din plan asociat unui număr complex pe un cerc de rază egală cu modulul numărului complex, modul egal cu lungimea (modulul) vectorului dec poziție al punctului reprezentat de numărul complex.

Cercul asociat unui număr complex constituie un loc geometric al numerelor complexe cu același modul.

Folosirea în probleme de geometrie

Numerele complexe pot fi folosite în probleme geometrice similar cu folosirea vectorilor euclidieni. Diferența a două numere complexe în forma algebrică este echivalentă cu un vector orientat de la punctul asociat celui de al doilea număr complex (care este al doilea termen al scăderii) către punctul asociat primului număr complex (care este primul termen al scăderii).

Folosirea numerelor complexe permite demonstrarea unor teoreme geometrice, de exemplu teorema bisectoarei.

Relații și operații cu numere complexe

• Egalitatea a două numere complexe z = (a,b) = a + bi și w = (c,d) = c + di are loc dacă a = c și b = d.

• Suma a două numere complexe z = (a,b) = a + bi și w = (c,d) = c + di este z + w = (a + c, b + d) = (a+c) + i(b+d). Pentru diferență componentele numărului complex care se scade sunt luate cu semnul minus, adică se adună opusul numărului complex care se scade.

• Produsul a două numere complexe z = (a,b)= a + bi și w = (c,d) = c + di este zw = (ac-bd,bc+ad) = (ac-bd) + i(bc+ad).
• Exemple: pentru z = (2,3) = 2 + 3i și w = (1,4) = 1 + 4i avem suma z + w = (3,7) = 3 + 7i și produsul zw = (-10,11) = -10 + 11i.

Numerele complexe permit factorizarea unei sume de pătrate similar procedeului de la diferență a două pătrate în produsul sumei prin diferență.

${\displaystyle a^{2}+b^{2}=(a+ib)(a-ib)}$

Împărțire

Numărul complex ${\displaystyle {\bar {z}}=x-iy}$ se numește conjugatul complex al numărului complex ${\displaystyle z=x+iy}$ (vezi mai jos).

Pentru fiecare număr complex ${\displaystyle a+bi,}$ în afară de zero, se poate găsi un număr complex ${\displaystyle {\frac {1}{a+bi}}.}$ invers lui^[1] Pentru aceasta înmulțesc numărătorul și numitorul fracției cu numărul complex ${\displaystyle a-bi,}$ conjugat numitorului: ${\displaystyle {\frac {1}{a+bi}}={\frac {a-bi}{(a+bi)(a-bi)}}={\frac {a-bi}{a^{2}+b^{2}}}={\frac {a}{a^{2}+b^{2}}}-{\frac {b}{a^{2}+b^{2}}}i.}$

Se definește rezultatul împărțirii numărului complex ${\displaystyle a+bi}$ cu un număr diferit de zero ${\displaystyle c+di\colon }$

${\displaystyle {\frac {a+bi}{c+di}}={\frac {\left(a+bi\right)\left(c-di\right)}{\left(c+di\right)\left(c-di\right)}}={\frac {ac+bd}{c^{2}+d^{2}}}+\left({\frac {bc-ad}{c^{2}+d^{2}}}\right)i.}$

Ca și în cazul numerelor reale, împărțirea poate fi înlocuită cu înmulțirea deîmpărțitului cu inversul divizorului.

Forma trigonometrică

Orice număr complex a cărui formă algebrică este ${\displaystyle z=a+bi}$ poate fi scris și sub formă trigonometrică, adică sub forma ${\displaystyle z=r\,(\cos \varphi +i\sin \varphi )\,}$, unde ${\displaystyle r={\sqrt {a^{2}+b^{2}}}}$ este modulul numărului complex z, iar ${\displaystyle \varphi =\arctan \left({\frac {b}{a}}\right)}$ este argumentul acestui număr complex .

Forma trigonometrică permite sublinierea rezultatului operațiilor de înmulțire, împărțire, ridicare la un exponent intreg și extragerea de radicali.

• ${\displaystyle z_{1}\cdot z_{2}=r_{1}\cdot r_{2}(\cos(t_{1}+t_{2})+i\sin(t_{1}+t_{2}))}$

• ${\displaystyle {z_{1} \over z_{2}}=}$ ${\displaystyle {r_{1} \over r_{2}}(\cos(t_{1}-t_{2})+i\sin(t_{1}-t_{2}))}$

• ${\displaystyle \ z^{n}=r^{n}(\cos(nt)+i\sin(nt))}$

• ${\displaystyle {\sqrt[{n\,}]{z}}={\sqrt[{n\,}]{r}}(\cos }$${\displaystyle {{t+2k\pi } \over {n}}+i\sin {{t+2k\pi } \over {n}})}$, k={0,1,2,... n-1}

Forma exponențială

Numărul complex a cărui formă trigonometrică este ${\displaystyle z=r\,(\cos \varphi +i\sin \varphi )\,}$ poate fi scris sub forma exponențială ${\displaystyle z=r\,\mathrm {e} ^{i\varphi }\,}$. Această posibilitate reiese din formula lui Euler.

Forma matricială

Mulțimea matricilor de dimensiuni ${\displaystyle 2\times 2}$ de forma: ${\displaystyle Z={\begin{pmatrix}a&-b\\b&a\end{pmatrix}}=a{\begin{pmatrix}1&0\\0&1\end{pmatrix}}+b{\begin{pmatrix}0&-1\\1&0\end{pmatrix}}=a\cdot E+b\cdot I}$ cu ${\displaystyle a,b\in \mathbb {R} }$ reprezintă de asemeni o formă de scriere a numerelor complexe, unde ${\displaystyle E}$ reprezintă matricea unitate și matricea ${\displaystyle I}$ reprezintă unitatea imaginară. Avem:

${\displaystyle \mathrm {Re} (Z)=a}$

${\displaystyle \mathrm {Im} (Z)=b}$

${\displaystyle I^{2}=-E}$ (analog cu ${\displaystyle \mathrm {i} ^{2}=-1}$)

${\displaystyle \operatorname {abs} (Z)={\sqrt {a^{2}+b^{2}}}={\sqrt {\det Z}}}$

Această mulțime reprezintă un subspațiu din spațiul vectorial al matricilor de dimensiuni ${\displaystyle 2\times 2}$.

Numerele reale corespund matricilor diagonale de forma

${\displaystyle {\begin{pmatrix}a&0\\0&a\end{pmatrix}}.}$

Conjugatul unui număr complex

• Conjugatul complex al unui numar ${\displaystyle \ z=a+bi}$ este numărul complex ${\displaystyle {\bar {z}}=a-bi}$ .
• Proprietățile conjugatului complex :
  • ${\displaystyle {\overline {\overline {z}}}=z}$
  • ${\displaystyle {\bar {z}}{\bar {w}}={\overline {zw}}}$
  • ${\displaystyle {\bar {z}}+{\bar {w}}={\overline {z+w}}}$
  • ${\displaystyle {\overline {(z/w)}}={\bar {z}}/{\bar {w}}}$ ${\displaystyle \Leftrightarrow }$ ${\displaystyle {\overline {\left({z \over w}\right)}}={{\bar {z}} \over {\bar {w}}}}$

Modulul unui număr complex

• Modulul numărului complex ${\displaystyle \ z=a+bi}$ este numărul real ${\displaystyle |z|={\sqrt {a^{2}+b^{2}}}}$. Este lungimea (modulul) vectorului poziție al afixului numărului complex.

• Proprietățile modulului:
  • ${\displaystyle |z|\geq 0,\forall z\in \mathbb {C} }$
  • ${\displaystyle |z|=0\Leftrightarrow z=0}$
  • ${\displaystyle |z_{1}\cdot z_{2}|=|z_{1}|\cdot |z_{2}|}$
  • ${\displaystyle |z_{1}+z_{2}|\leq |z_{1}|+|z_{2}|}$ (inegalitatea triunghiului)
  • ${\displaystyle |z_{1}\cdot z_{2}\cdot ...\cdot z_{n}|=|z_{1}|\cdot |z_{2}|\cdot ...\cdot |z_{n}|}$
  • ${\displaystyle |z_{1}^{n}|={|z_{1}|}^{n}}$
  • ${\displaystyle \left|{\frac {z_{1}}{z_{2}}}\right|={{|z_{1}|} \over {|z_{2}|}}}$
  • Are loc identitatea ${\displaystyle |z|^{2}=z{\bar {z}}}$ și deci ${\displaystyle {1 \over z}={{\bar {z}} \over {|z|^{2}}}}$ , dacă ${\displaystyle \ z\neq 0}$
  • ${\displaystyle |\pm i|=1}$.

Puterile și radicalii numerelor complexe

Puterile lui i

${\displaystyle \ i^{2}=-1}$${\displaystyle \ =>}$${\displaystyle \ i^{3}=}$${\displaystyle \ i^{2}\cdot i=i\cdot (-1)=-i}$

${\displaystyle \ i^{3}=-i}$${\displaystyle \ =>}$${\displaystyle \ i^{4}=}$${\displaystyle \ i^{3}\cdot i=i\cdot (-i)=1}$

Generalizare:

• ${\displaystyle \ i^{n}=1}$ cu ${\displaystyle \ n}$ de forma ${\displaystyle \ 4k}$

• ${\displaystyle \ i^{n}=i}$ cu ${\displaystyle \ n}$ de forma ${\displaystyle \ 4k+1}$

• ${\displaystyle \ i^{n}=-1}$ cu ${\displaystyle \ n}$ de forma ${\displaystyle \ 4k+2}$

• ${\displaystyle \ i^{n}=-i}$ cu ${\displaystyle \ n}$ de forma ${\displaystyle \ 4k+3}$

Puterile naturale ale numerelor complexe

Pentru puteri naturale ${\displaystyle n}$ ale numerelor complexe scrise sub forma polară ${\displaystyle z=r\cdot e^{i\cdot \varphi }}$ există formula de calcul:

• ${\displaystyle z^{n}=r^{n}\cdot e^{i\cdot n\cdot \varphi }}$

sau, folosind forma algebrică a numerelor complexe ${\displaystyle z=a+i\cdot b}$, se obține prin binomul lui Newton

• ${\displaystyle z^{n}=\sum _{k=0,k\,par}^{n}{n \choose k}\cdot (-1)^{\frac {k}{2}}\cdot a^{n-k}\cdot b^{k}+i\sum _{k=1,k\,impar}^{n}{n \choose k}\cdot (-1)^{\frac {k-1}{2}}\cdot a^{n-k}\cdot b^{k}}$,

unde ${\displaystyle {n \choose k}=C_{n}^{k}}$ reprezintă coeficientul binomial (numărul de combinări de ${\displaystyle n}$ elemente luate câte ${\displaystyle k}$).

Puterile complexe ale numerelor complexe

Dacă baza ${\displaystyle z}$ și exponentul ${\displaystyle \omega }$ al puterii sunt ambele numere complexe, atunci

• ${\displaystyle z^{\omega }:=e^{\omega \cdot \ln z}}$

Radicalii numerelor complexe

În privința calculului cu radicali ai numerelor complexe, nu mai sunt valabile regula semnelor de la numere reale nenegative pentru produse și câturi sub radical. Indiferent care din cele două valori se folosesc, i sau ${\displaystyle -i=-{\sqrt {-1}}}$ se obține:

${\displaystyle 1={\sqrt {1}}={\sqrt {(-1)\cdot (-1)}}\neq {\sqrt {-1}}\cdot {\sqrt {-1}}=-1}$

Pentru calculul radicalului de ordinul n al unui număr complex ${\displaystyle z=re^{\mathrm {i} \phi }}$ se folosește formula

${\displaystyle {\sqrt[{n}]{z}}={\sqrt[{n}]{r}}\,e^{\mathrm {i} {\frac {\phi +2k\pi }{n}}}}$,

unde k ia valorile ${\displaystyle 0,1,\ldots ,n-1}$. Un număr complex are deci n rădăcini complexe. Astfel, radicalul unui număr complex nu este unic determinat.

Logaritmul unui număr complex

Numărul complex ${\displaystyle w}$ este un logaritm natural al numărului complex ${\displaystyle z\neq 0}$ dacă

${\displaystyle e^{w}=z}$.

Urmărește că dacă ${\displaystyle w}$ este un logaritm natural a lui z, atunci fiecare dintre numerele ${\displaystyle w+2k\pi \mathrm {\,} i}$, cu ${\displaystyle k\in \mathbb {Z} }$, este și el un logaritm natural a lui z. Cu alte cuvinte, logaritmul natural al unui număr complex nu este unic determinat, iar logaritmii naturali ai lui z sunt numerele

${\displaystyle \ln(z)=\ln |z|+\mathrm {i} \,\mathrm {arg} (z),}$

unde ${\displaystyle \ln |z|}$ este logaritmul natural (unic) al numărului real ${\displaystyle z}$, și ${\displaystyle \mathrm {arg} (z)}$ este un argument (neunic) a lui ${\displaystyle z}$.

Pentru a obține o valoare unică a logaritmului, se poate folosi în formula precedentă valoarea principală a argumentului — adică unicul argument ${\displaystyle \phi }$ al lui ${\displaystyle z}$ astfel încât ${\displaystyle \phi \in ]-\pi ,\pi ].}$ Prin convenție, valoare principală a argumentului se notează cu majusculă, pentru a o diferenția din altele argumente:

${\displaystyle \mathrm {Arg} (z)\in ]-\pi ,\pi ]\quad }$ și ${\displaystyle \quad \mathrm {Arg} (z)=\mathrm {arg} (z)+2k\pi \mathrm {,} \;k\in \mathbb {Z} .}$

Se numește valoarea principală a logaritmului natural numărul complex

${\displaystyle \mathrm {Ln} (z)=\ln |z|+\mathrm {i} \,\mathrm {Arg} (z).}$

Ca pentru valoarea principală a argumentului, valoarea principală a logaritmului natural se notează cu majusculă, pentru a o diferenția din alți logaritmi.

Formulat altfel, dacă ${\displaystyle z=re^{\mathrm {i} \phi }}$, unde ${\displaystyle r>0}$ și ${\displaystyle -\pi <\phi \leq \pi }$, atunci valoarea principală a logaritmului lui ${\displaystyle z}$ este

${\displaystyle \mathrm {Ln} (z)=\ln r+\mathrm {i} \phi }$.

Formula lui Euler și identitatea lui Euler

Pornind de la reprezentarea funcțiilor sinus și cosinus pe cercul trigonometric se poate ajunge la formula lui Euler care exprimă un număr complex de modul unitate (rădăcină a unității) prin intermediul funcției exponențiale:

${\displaystyle \mathrm {e} ^{i\varphi }=\cos \varphi +i\sin \varphi \,}$

În cazul particular în care φ = π se obține identitatea lui Euler.^[2]

${\displaystyle \mathrm {e} ^{i\pi }=-1}$

Note

Bibliografie

• Nicolae Mihăileanu, Istoria matematicii, volumul II, Editura Științifică și Enciclopedică, București, 1981, p. 206-208
• en Lars Ahlfors (1979). Complex analysis. An introduction to the theory of analytic functions of one complex variable (ed. Third edition). Harvard University: McGraw-Hill Book Company. p. 317. ISBN 0-07-000657-1. Mentenanță CS1: Text în plus (link)
• ***, Manual de Algebră pentru clasa a IX-a, 1988

Vezi și

• Cuaternion
• Formula lui Euler
• Formula lui Moivre
• Transformare geometrică

Legături externe

• en John and Betty's Journey Through Complex Numbers
• en SOS Math - Complex Variables
• en Algebraic Structure of Complex Numbers de la situl cut-the-knot
• en A history of complex numbers.
• en Eric W. Weisstein, Complex Number la MathWorld.

	Matematică – Teoria numerelor --- Matematică discretă (categorie)
	Matematicieni specializați în Teoria numerelor (categorie)  • • ${\displaystyle \mathbb {N} }$  • • ${\displaystyle \mathbb {Z} }$  • • ${\displaystyle \mathbb {Q} }$  • • ${\displaystyle \mathbb {I} }$  • • ${\displaystyle \mathbb {T} }$  • • ${\displaystyle \mathbb {R} }$  • • ${\displaystyle \mathbb {C} }$  • •