Função de Lagrange

Mecânica clássica
Diagramas de movimento orbital de um satélite ao redor da Terra, mostrando a velocidade e aceleração.
Cinemática Deslocamento Velocidade Velocidade escalar Aceleração Aceleração centrípeta Movimento uniforme Movimento uniformemente variado Movimento retilíneo Movimento parabólico Movimento circular Movimento circular uniforme Movimento curvilíneo Movimento harmônico simples Movimento harmônico complexo
Dinâmica Força Inércia Produto de inércia Leis de Newton Primeira Lei de Newton Segunda Lei de Newton Terceira Lei de Newton Equações de movimento Ressonância
História História da física
Trabalho e Mecânica Energia cinética Energia potencial Trabalho Conservação da energia Força conservativa Força de contato Função de Lagrange Potência Retropropulsão Princípio de Hamilton
Sistema de partículas Centro de massa Corpo rígido Momento linear Conservação do momento linear Equilíbrio dinâmico Princípio de d'Alembert Sistema massa-mola
Colisões Impulso Colisão elástica Colisão inelástica
Movimento rotacional Posição angular Deslocamento angular Velocidade angular Aceleração angular Momento de inércia Torque Momento angular
Sistemas Clássicos Sistema dinâmico Sistema linear Sistema não linear Sistema hamiltoniano Sistema caótico
Formulações Mecânica newtoniana Mecânica hamiltoniana Mecânica lagrangiana Mecânica KvN Equação de Udwadia-Kalaba Mecânica de Routhian
Gravitação Lei da gravitação universal Princípio da superposição Constante gravitacional Velocidade de escape Leis de Kepler Princípio da equivalência
Físicos Isaac Newton Leonhard Euler Joseph-Louis Lagrange Pierre-Simon Laplace Galileu Galilei William Rowan Hamilton Johannes Kepler
v d e

Na mecânica clássica, a função de Lagrange, lagrangiana ^{(português brasileiro)} ou lagrangiano ^{(português europeu)} (${\displaystyle {\mathcal {L}}}$) de um sistema é uma função expressa em termos das coordenadas generalizadas ${\displaystyle q_{i}}$, da taxa de variação dessas coordenadas (velocidades generalizadas) ${\displaystyle {\dot {q}}_{i}}$ e do tempo t, e dada matematicamente pela diferença entre a energia cinética (${\displaystyle T}$) e a energia potencial generalizada (${\displaystyle U}$) do sistema:

${\displaystyle {\mathcal {L}}_{(q_{i},{\dot {q}}_{i},t)}=T-U}$.^{[Ref. 1][Ref. 2][Ref. 3]}

Por padrão a energia potencial é função apenas das coordenadas generalizadas (sistemas conservativos) e/ou do tempo, contudo, a exemplo do que observa-se para o caso eletromagnético, quando na forma adequada, admite-se o uso de um potencial "generalizado", que é função também das velocidades generalizadas. O potencial eletromagnético generalizado^{[1][Ref. 3]} permite a descrição de partículas elétricas imersas em campos eletromagnéticos via Mecânica de Lagrange, a exemplo. Forças dissipativas proporcionais às velocidades generalizadas também são admissíveis via potenciais dissipativos, a exemplo o potencial dissipativo de Rayleigh.^{[2][3] [Ref. 3]}

A lagrangiana é termo central na integral temporal que define o que se denomina em Física por ação. Diferente da Mecânica de Newton, junto com o princípio de Hamilton da ação em extremo, a lagrangiana e a Mecânica de Lagrange definem toda a dinâmica de um sistema sem recorrer a vetores e diagramas vetoriais, fazendo-o de forma a usar essencialmente funções escalares. Nesses termos a lagrangiana porta-se como uma equação fundamental do sistema a qual associa-se, encerrando em si todas as informações acerca do sistema. Pode-se pois, a partir dela e do formalismo atrelado à Mecânica de Lagrange, obter qualquer informação desejada acerca do sistema. A lagrangiana possui dimensões de energia, joules no S.I..^{[Ref. 1][Ref. 2][Ref. 3]}

Associado à lagrangiana de um sistema, via Transformada de Legendre, tem-se o hamiltoniano ${\displaystyle {\mathcal {H}}}$ do sistema, essa uma função das coordenadas generalizadas ${\displaystyle q_{i}}$, dos momentos conjugados generalizados ${\displaystyle p_{i}}$ e do tempo t. O Hamiltoniano ${\displaystyle H_{(q_{i},p_{i},t)}}$, definido por H = T + U, também caracteriza uma equação fundamental, e juntamente com o formalismo da Mecânica de Hamilton, constitui formalismo alternativo plenamente equivalente ao de Lagrange no que tange à descrição da dinâmica do sistema.^{[Ref. 2]} Tais formalismos encontram importante aplicação também dentro da relatividade.^{[Ref. 4]}

Embora amplamente aplicada ao campo da dinâmica de energia e matéria, o cálculo variacional não limita o raciocínio à campos específicos da Física. Diversos problemas nas mais variadas áreas mostram-se suscetíveis ao tratamento similar.

Exemplos

Mecânica

Partícula livre

Uma partícula livre move-se em ausência de força resultante, idealmente em ausência de força aplicada. Logo sua lagrangiana define-se apenas por sua energia cinética em caso limite.

${\displaystyle {\mathcal {L}}=T-U=T={\frac {1}{2}}m[{\dot {x}}^{2}+{\dot {y}}^{2}+{\dot {z}}^{2}]}$

onde, conforme convenção, ${\displaystyle {\dot {x}}={\frac {dx}{dt}}=v_{x}}$ e assim por diante.

Para movimento confinado ao plano xy, e em coordenadas polares:

${\displaystyle x=r\cos \theta }$

${\displaystyle y=r\sin \theta }$

de onde, derivando-se:

${\displaystyle {\dot {x}}={\dot {r}}\cos \theta -r{\dot {\theta }}\sin \theta }$

${\displaystyle {\dot {y}}={\dot {r}}\sin \theta +r{\dot {\theta }}\cos \theta }$

Quadrando-se as velocidades generalizadas e com o auxílio de algumas relações trigonométricas tem-se pois que:

${\displaystyle {\mathcal {L}}_{(r,{\dot {r}},\theta ,{\dot {\theta }},t)}={\frac {1}{2}}m[{\dot {r}}^{2}+{(r{\dot {\theta }})}^{2}]}$

Máquina de Atwood

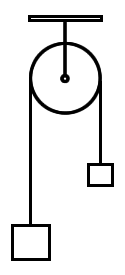
Na máquina de Atwood, considerando g a aceleração da gravidade, M₁ a massa da esquerda e M₂ a massa da direita, a energia potencial do sistema escreve-se:

${\displaystyle U=-M_{1}gx-M_{2}gy}$ ,

uma vez adotado o nível de referência como sendo uma linha horizontal a passar pelo centro do disco. Nessa situação x e y representam os tamanhos em suspensão da corda que sustentam respectivamente as massas M₁ e M₂.

Há um vínculo entre x e y de tal forma que ${\displaystyle x+y=c}$ é uma constante, o tamanho total de corda em suspensão. Nesses termos, basta uma coordenada generalizada para descrever-se o problema, à escolha, x, e reescreve-se a energia potencial gravitacional como:

${\displaystyle U=-M_{1}gx-M_{2}g(c-x)}$

Em uma máquina de Atwood ideal a polia e a corda têm massas desprezíveis se comparadas às massas M₁ e M₂. Nesse caso a energia cinética total se escreve:

${\displaystyle T={\frac {1}{2}}M_{1}\left({\frac {dx}{dt}}\right)^{2}+{\frac {1}{2}}M_{2}\left({\frac {d(c-x)}{dt}}\right)^{2}={\frac {1}{2}}(M_{1}+M_{2}){\dot {x}}^{2}}$

e a função de Lagrange escreve-se:

${\displaystyle L_{(x,{\dot {x}},t)}=T-U={\frac {1}{2}}(M_{1}+M_{2}){\dot {x}}^{2}+M_{1}gx+M_{2}g(c-x)}$

que encerra em si toda informação necessária ao cálculo da dinâmica do sistema.

Seguindo-se com o formalismo de Lagrange, tem-se que a equação de movimento deve satisfazer à equação de Lagrange:

${\displaystyle {\frac {d}{dt}}\left({\frac {\partial L}{\partial {\dot {q}}_{i}}}\right)-{\frac {\partial L}{\partial q_{i}}}=0}$ .

Neste caso há apenas uma coordenada generalizada, q_i = x. Determinando-se as derivadas tem-se:

${\displaystyle {\frac {\partial L}{\partial x}}=(M_{1}-M_{2})g}$

${\displaystyle {\frac {\partial L}{\partial {\dot {x}}}}=(M_{1}+M_{2}){\dot {x}}}$

${\displaystyle {\frac {d}{dt}}\left({\frac {\partial L}{\partial {\dot {x}}}}\right)=(M_{1}+M_{2}){\ddot {x}}}$

Levando os resultados à equação de Lagrange tem-se a equação diferencial para o sistema:

${\displaystyle {\ddot {x}}=a={\frac {M_{1}-M_{2}}{M_{1}+M_{2}}}g}$

onde a é a aceleração das massas. Tal equação é análoga à obtida via aplicações diretas da lei de Newton conforme descrito em artigo específico, conforme esperado.

A equação horária para x obtém-se com facilidade doravante mediante integração, sendo a resposta análoga à de um movimento retilíneo uniformemente variado com aceleração constante ${\displaystyle a={\ddot {x}}}$:

${\displaystyle x_{(t)}=X_{0}+V_{0}t+{\frac {1}{2}}\left({\frac {M_{1}-M_{2}}{M_{1}+M_{2}}}g\right)t^{2}}$

com ${\displaystyle X_{0}}$ e ${\displaystyle V_{0}}$ correspondendo a constantes, respectivamente o comprimento em suspensão inicial da corda para a massa M₁ e a velocidade descendente inicial (no sentido de x crescente) da massa M₁, determinados no instante em que zera-se o tempo (t=0s).

Microeconomia

Na microeconomia a função lagrangiana (ou simplesmente lagrangiano) é uma função utilizada para resolver problemas de otimização com restrição, tanto em mecânica quanto em outras áreas não necessariamente da física.

Suponha uma economia com apenas dois bens, banana (b) e abacate (a). Pode-se querer maximizar a utilidade, grosso modo a satisfação do consumidor - no problema representada pela função "u", que é logaritmicamente tanto maior quanto maior for o consumo dos bens banana e abacate - mantida contudo uma restrição orçamentária especificada.

O problema resume-se pois em:

• ${\displaystyle \max u\left(q_{a},q_{b}\right)=\max {\underbrace {\left(\ln(q_{a})+\ln(q_{b})\right)} _{u(q_{a},q_{b})}}}$

com ${\displaystyle q_{b},q_{a}}$ representando a quantidade consumida de banana e de abacate respectivamente, e o símbolo ${\displaystyle ln}$ representa o logaritmo neperiano, isso sob uma restrição orçamentária que traduz-se em linguagem matemática por:

• ${\displaystyle p_{a}\times q_{a}+p_{b}\times q_{b}\leq S}$,

com ${\displaystyle p_{b},p_{a}}$ correspondendo aos preços de banana e abacate respectivamente e S ao salário do consumidor em questão.

Pela lei de Walras, esta desigualdade vale como igualdade, ou seja, o consumidor gastará todo o seu salário.

O lagrangiano deste problema fica então^[4]:

${\displaystyle L\left(x_{1},x_{2},\mu \right)\equiv \underbrace {\left(\ln(q_{a})+\ln(q_{b})\right)} _{u(q_{a},q_{b})}-\mu \left(p_{a}\times q_{a}+p_{b}\times q_{b}-S\right)}$

A variável ${\displaystyle \mu }$ que multiplica a restrição é chamada de multiplicador de lagrange.^[4]

A quantidade ótima de consumo ${\displaystyle (q_{a}^{*},q_{b}^{*})}$ que resolve este problema atende a três condições:

${\displaystyle {\frac {\partial L}{\partial \mu }}=0\rightarrow \left(p_{a}\times q_{a}+p_{b}\times q_{b}-S\right)=0}$

${\displaystyle {\frac {\partial L}{\partial q_{a}}}=0\rightarrow \underbrace {{\frac {1}{q_{a}}}\times 1} _{\frac {\partial ln(q_{a})}{\partial q_{a}}}+\left(-\mu p_{a}\right)=0}$

${\displaystyle {\frac {\partial L}{\partial q_{b}}}=0\rightarrow \underbrace {{\frac {1}{q_{b}}}\times 1} _{\frac {\partial ln(q_{b})}{\partial q_{b}}}+\left(-\mu p_{b}\right)=0}$

Referências

• Outras referências:

Ver também

• Mecânica Lagrangiana
• Multiplicadores de Lagrange
• Joseph-Louis Lagrange

• Portal da ciência
• Portal da física