Sterkteleer

Sterkteleer of toegepaste mechanica onderzoekt de voorwaarden waaraan constructies moeten voldoen om niet te bezwijken, de gewenste stijfheid te hebben en voldoende duurzaam te zijn.

Sterkteleer valt uiteen in elasticiteitsleer, plasticiteitsleer en breukleer, waarbij gebruik wordt gemaakt van theoretische mechanica, wiskunde en materiaalkunde. Sterkteleer is belangrijk bij het ontwerp van stilstaande en bewegende constructies in de werktuigkunde, bouwkunde en de civiele techniek.

Basisbegrippen

Belastingen

Een belasting is het geheel van krachten en momenten dat inwerkt op een voorwerp of constructie. De belastingen die door een constructie moeten kunnen worden weerstaan, zijn:

• nuttige belasting, die volgt uit de functie van de constructie;
• eigen gewicht;
• toevallige belastingen, zoals wind of sneeuw;
• steunpuntsreacties.

Dit geheel zijn de uitwendige krachten. Een belasting kan op verschillende manieren op de constructie werken:

• volumebelasting;
• oppervlaktebelasting;
• lijnlast;
• puntlast;
• verdeelde belasting:
  • gelijkmatig verdeelde belasting;
  • lineair verlopende belasting;
  • willekeurig verlopende belasting;
• koppel.

Inwendige krachten en koppels

Een belasting veroorzaakt een vormververandering. Zodra de belasting weggenomen wordt, zal het voorwerp zijn nieuwe vorm behouden of geheel of gedeeltelijk zijn oude vorm hernemen. De mate waarin dit gebeurt, hangt af van de veerkracht of elasticiteit van het materiaal. Deze wordt bepaald door de cohesie van de moleculen, waardoor er inwendige krachten optreden bij vormverandering. Deze inwendige krachten zijn onder te verdelen in:

• een normaalkracht ${\displaystyle F_{\text{n}}}$ die loodrecht op de dwarsdoorsnede staat. Hierbij wordt onderscheid gemaakt tussen een trekkracht van de dwarsdoorsnede af en een drukkracht naar de dwarsdoorsnede toe;
• een buigend koppel die loodrecht werkt op de dwarsdoorsnede, waarbij de grootte wordt uitgedrukt als buigend moment ${\displaystyle M_{\text{b}}}$;
• een dwarskracht ${\displaystyle F_{\text{d}}}$, ook wel schuifkracht genoemd, die zich in het vlak van de dwarsdoorsnede bevindt;
• een wringend koppel dat in het vlak van de dwarsdoorsnede werkt, waarbij de grootte wordt uitgedrukt als wringend moment ${\displaystyle M_{\text{w}}}$.

Spanningen

Een kracht ${\displaystyle F}$ die op een oppervlakte ${\displaystyle A}$ werkt, veroorzaakt een spanning ${\displaystyle \sigma }$:

${\displaystyle \sigma ={\frac {F}{A}}}$

Net als kracht, is spanning een richtingsgrootheid. Een willekeurig gerichte spanning kan onderverdeeld worden in een normaalspanning ${\displaystyle \sigma }$ – trek- dan wel drukspanning – en een schuifspanning of wringspanning ${\displaystyle \tau }$.

Elasticiteitsmodulus

De optredende vervormingen zullen elastische vervorming veroorzaken tot de vloeigrens, waarboven onomkeerbare plastische vervorming optreedt. In het elastisch gebied geldt de wet van Hooke, waarbij de rek ${\displaystyle \varepsilon }$ die optreedt lineair afhankelijk is van de aangebrachte spanning ${\displaystyle \sigma }$, met als evenredigheidsconstante de elasticiteitsmodulus ${\displaystyle E}$:

${\displaystyle \varepsilon ={\sigma \over E}}$

${\displaystyle \varepsilon }$ wordt bepaald met de trekproef en uitgezet tegen de spanning in een trekkromme.

Kwadratisch oppervlaktemoment

De weerstand tegen buiging, wringing en knik wordt bepaald door het kwadratisch oppervlaktemoment of oppervlaktetraagheidsmoment.

Buiging en afschuiving

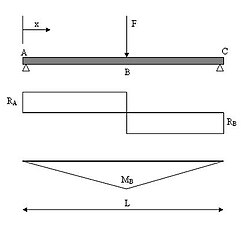
Soorten lastgevallen

Bij stilstaande of statische kracht is er een soort lastgeval: in rust. Bij bewegende of dynamische kracht zijn er twee soorten lastgevallen: de golvende en wisselende.

• in rust: De belasting van het bouwelement verandert niet, bijvoorbeeld draagkabel, pijler
• golvend: Het bouwelement wordt in één richting belast of ontspannen, bijvoorbeeld kabels van hefwerktuigen
• wisselend: De belasting van het bouwelement gebeurt in wisselende richting, bijvoorbeeld as op wisselende buiging

De verschillende soorten belastingen

De aard en hun formules.

Trek en druk

Formules voor enkelvoudige trek en/of druk

Normaalspanning

${\displaystyle \sigma ={\frac {F}{A}}}$

Rek (verlenging per lengte-eenheid)

${\displaystyle \varepsilon ={\frac {\sigma }{E}}={\frac {F}{EA}}}$

De factor ${\displaystyle EA}$ is de rekstijfheid.

Verlenging voor homogene doorsneden

${\displaystyle \delta =\int \limits _{0}^{L}\varepsilon \,\mathrm {d} x=\int \limits _{0}^{L}{\frac {\sigma }{E}}\,\mathrm {d} x=\int \limits _{0}^{L}{\frac {F}{E\cdot A}}\,\mathrm {d} x}$

Als ${\displaystyle E}$ en ${\displaystyle A}$ constant zijn, is:

${\displaystyle \delta ={\frac {F\cdot L}{E\cdot A}}}$

Daarin is:

• σ: de normaalspanning (trek of druk) in N/mm²,
• F: de trek- of drukkracht in N,
• E: de elasticiteitsmodulus in N/mm²,
• δ: de verlenging in mm,
• ε: de langsrek (verlenging per lengte-eenheid),
• A: de oppervlakte van de dwarsdoorsnede in mm²;
• L: de lengte in mm.

Buiging

formules

Normaalspanning

${\displaystyle \sigma ={\frac {M_{b}\cdot y}{I}}}$

met

${\displaystyle I=\int \limits _{A}y^{2}\,\mathrm {d} A}$

Rek (verlenging per lengte-eenheid)

${\displaystyle \varepsilon ={\frac {\sigma }{E}}={\frac {y}{\rho }}}$

Kromming van de neutrale vezel

${\displaystyle \rho ^{-1}={\frac {M_{b}}{EI}}}$

De factor ${\displaystyle EI}$ is de buigstijfheid.

Daarbij is:

• σ: de normaalspanning in een punt in N/mm²,
• M_b: het buigmoment op de dwarsdoorsnede in Nmm,
• y: de afstand tot de neutrale vezel in mm,
• I: het oppervlaktetraagheidsmoment in mm⁴,
• ε: de rek (verlenging per lengte-eenheid) in mm/mm,
• ρ: de kromtestraal van de neutrale vezel in mm,
• A: de oppervlakte van de dwarsdoorsnede in mm²,
• E: de elasticiteitsmodulus in N/mm².

Afschuiving

Vereenvoudigde formules

Onderstaande vereenvoudigde formules zijn alleen toepasbaar op klinknagels, bout- en lasverbindingen en andere situaties waar de dwarskracht rechtstreeks aangrijpt in het vlak van de afschuiving.

Schuifspanning

${\displaystyle \tau ={\frac {T}{A}}}$

Glijdingshoek

${\displaystyle \gamma ={\frac {\tau }{G}}={\frac {T}{GA}}}$

Daarbij is:

• τ: de schuifspanning in een punt,
• T: de dwarskracht op de dwarsdoorsnede,
• A: de oppervlakte van de dwarsdoorsnede,
• G: de glijdingsmodulus,
• γ: de glijdingshoek.

Formule voor afschuiving bij balken

De vereenvoudigingen zoals hierboven zijn niet toepasbaar op balken. Hiervoor werd een verbeterde theorie opgesteld, de theorie van Jourawski.

Schuifspanning in een punt

${\displaystyle \tau ={\frac {T\cdot S}{b\cdot I}}}$

Daarbij is:

• τ: de schuifspanning in een punt,
• T: de dwarskracht op de dwarsdoorsnede,
• S: het statisch moment ten opzichte van het beschouwde punt,
• I: het oppervlaktetraagheidsmoment,
• b: de breedte van de dwarsdoorsnede ter hoogte van het beschouwde punt.

Wringing (torsie)

formules

Voor cirkelvormige dwarsdoorsnedes gelden volgende formules:

schuifspanning

${\displaystyle \tau ={\frac {M_{w}\cdot \rho }{I_{p}}}}$

met

${\displaystyle I_{p}=\int \limits _{A}\rho ^{2}\,\mathrm {d} A}$

wringingshoek per lengte-eenheid

${\displaystyle \theta ={\frac {M_{w}}{G\,I_{p}}}}$

De factor ${\displaystyle G\,I_{p}}$ heet de wringstijfheid.

rotatiehoek van verschillende dwarsdoorsnedes ${\displaystyle A}$ en ${\displaystyle >B}$ ten opzichte van elkaar

${\displaystyle \psi _{A-B}=\int \limits _{A}^{B}\theta \,\mathrm {d} x=\int \limits _{A}^{B}{\frac {M_{w}}{G\,I_{p}}}\,\mathrm {d} x}$

Voor constante doorsnedes en wringmoment wordt dit

${\displaystyle \psi _{A-B}={\frac {M_{w}\,L}{G\,I_{p}}}}$

Daarbij is:

• τ: de schuifspanning in een punt in N/mm²,
• M_w: het wringmoment op de dwarsdoorsnede in Nmm,
• ρ: de afstand tot het middelpunt van de dwarsdoorsnede in mm,
• I_p: het polair traagheidsmoment in mm⁴,
• A: de oppervlakte van de dwarsdoorsnede in mm²,
• θ: de wringingshoek per lengte-eenheid in radiaal/mm,
• G: de glijdingsmodulus in N/mm²,
• L: de afstand tussen de dwarsdoorsnedes ${\displaystyle A}$ en ${\displaystyle >B}$ in mm,
• ψ: de rotatiehoek in radialen.

Diepergaande uitleg

Een diepergaande behandeling van de sterkteleer is te vinden in het Wikibook Sterkteleer.

Zie ook

Publicaties

• Adolf Lubbertus Bouma, Toegepaste mechanica : wetenschap of gereedschap?, Delftse Universitaire Pers, 1986.
• Jelle Witteveen, Lessen uit de geschiedenis van de toegepaste mechanica, Intreerede TH Delft, Delftse Universitaire Pers, 1976.