点と直線の距離

ユークリッド幾何学において点と直線の距離 (てんとちょくせんのきょり、英: Distance from a point to a line) とは、点と直線上の任意の点の距離で最短になるものをいう。点と直線を結ぶ線分で点と直線の距離に等しい長さをもつものは、与えられた直線と直交する性質がある。点と直線の距離を計算する公式は、いくつかの方法によって導出できる。

点と直線の間の最短距離を知ることは様々な場面において有益である。例えば、道路までの最短距離が分かったり、グラフ上の値のちらばりを定量化したりなどである。線形曲線回帰の一種であるデミング回帰（英語版）では、独立変数と従属変数が等しい分散を持つ場合には、近似曲線と各データ点の距離によって近似の精度が測定される直交回帰（英語版）に帰着される。

デカルト座標における距離

方程式で定義された直線

ax + by + c = 0の形の方程式により平面上の直線が与えられた場合(但し a, b, c は実数の定数で a, b は非零である)、点 (x0, y0) と直線の距離は

distance ⁡ ( a x + b y + c = 0 , ( x 0 , y 0 ) ) = | a x 0 + b y 0 + c | a 2 + b 2 {\displaystyle \operatorname {distance} (ax+by+c=0,(x_{0},y_{0}))={\frac {|ax_{0}+by_{0}+c|}{\sqrt {a^{2}+b^{2}}}}}

となる[1][2]:p.14。また直線上の点で、(x0, y0) に最も近い点の座標は以下で与えられる[3]:

x = b ( b x 0 − a y 0 ) − a c a 2 + b 2  and  y = a ( − b x 0 + a y 0 ) − b c a 2 + b 2 . {\displaystyle x={\frac {b(bx_{0}-ay_{0})-ac}{a^{2}+b^{2}}}{\text{ and }}y={\frac {a(-bx_{0}+ay_{0})-bc}{a^{2}+b^{2}}}.}

軸に平行な直線

一般の直線の方程式 ax + by + c = 0 について、c が 0 でない限り a と b がともに 0 になることはない。またそのような場合、方程式はもはやどんな直線も定めない。もし a = 0, b ≠ 0 のときには直線は x 軸に平行で、方程式は y = −c/b となる。この直線と点 (x0, y0) の距離は、上の等式にあてはめることにより長さ |y0 − (−c/b)| = |by0 + c|/|b| の x 軸に垂直な線分から得られる。同様に x 軸に垂直な直線 (b = 0) と点 (x0, y0) との距離も、長さ|ax0 + c|/|a| の x 軸に平行な線分から得られる。

直線が通る2点によって定義された直線

点 P1=(x1,y1) P2=(x2,y2)の2点を通過する直線と点(x0、y0)の距離は以下で与えられる:

distance ⁡ ( P 1 , P 2 , ( x 0 , y 0 ) ) = | ( y 2 − y 1 ) x 0 − ( x 2 − x 1 ) y 0 + x 2 y 1 − y 2 x 1 | ( y 2 − y 1 ) 2 + ( x 2 − x 1 ) 2 . {\displaystyle \operatorname {distance} (P_{1},P_{2},(x_{0},y_{0}))={\frac {|(y_{2}-y_{1})x_{0}-(x_{2}-x_{1})y_{0}+x_{2}y_{1}-y_{2}x_{1}|}{\sqrt {(y_{2}-y_{1})^{2}+(x_{2}-x_{1})^{2}}}}.}

分母は、点P1と点P2の距離である。分子は、直線上の2点と点(x0,y0)を頂点とする三角形の面積の2倍になっている(参照:en:Area of a triangle#Using coordinates)。 この公式は、三角形の面積を求める公式 A = 1 2 b h {\textstyle A={\frac {1}{2}}bh} を変形して得られる h = 2 A b {\textstyle h={\frac {2A}{b}}} と同値である。但しbは三角形の底辺の長さを、hはその底辺に対する三角形の高さを表す。

証明

代数的な証明

この証明は、直線が座標軸に対して平行でも垂直でもない場合にのみ、つまり直線の方程式でaもbも0でない場合にのみ成り立つ証明である。

方程式 ax + by + c = 0 で表される直線の傾きは −a/b であるから、この直線に対して垂直な任意の線分の傾きはb/a (与えられた直線の傾きの逆数の負)である。ここで点(m, n)を、与えられた直線と、点(x0, y0)を通り与えられた直線に直交する直線の交点とする。点(m, n)と点(x0, y0)を通る直線は元の直線に直交するから

y 0 − n x 0 − m = b a . {\displaystyle {\frac {y_{0}-n}{x_{0}-m}}={\frac {b}{a}}.}

したがって a ( y 0 − n ) − b ( x 0 − m ) = 0 {\displaystyle a(y_{0}-n)-b(x_{0}-m)=0}  が得られ、さらに両辺を2乗することで以下を得る：

a 2 ( y 0 − n ) 2 + b 2 ( x 0 − m ) 2 = 2 a b ( y 0 − n ) ( x 0 − m ) . {\displaystyle a^{2}(y_{0}-n)^{2}+b^{2}(x_{0}-m)^{2}=2ab(y_{0}-n)(x_{0}-m).}

ここで、次の等式を考える。但し第2式から第3式への変形には、上の2乗した等式を用いた。

( a ( x 0 − m ) + b ( y 0 − n ) ) 2 = a 2 ( x 0 − m ) 2 + 2 a b ( y 0 − n ) ( x 0 − m ) + b 2 ( y 0 − n ) 2 = ( a 2 + b 2 ) ( ( x 0 − m ) 2 + ( y 0 − n ) 2 ) . {\displaystyle (a(x_{0}-m)+b(y_{0}-n))^{2}=a^{2}(x_{0}-m)^{2}+2ab(y_{0}-n)(x_{0}-m)+b^{2}(y_{0}-n)^{2}=(a^{2}+b^{2})((x_{0}-m)^{2}+(y_{0}-n)^{2}).}

 一方で、点(m, n)がax + by + c =0上にあることから、次の式も成り立つ：

( a ( x 0 − m ) + b ( y 0 − n ) ) 2 = ( a x 0 + b y 0 − a m − b n ) 2 = ( a x 0 + b y 0 + c ) 2 . {\displaystyle (a(x_{0}-m)+b(y_{0}-n))^{2}=(ax_{0}+by_{0}-am-bn)^{2}=(ax_{0}+by_{0}+c)^{2}.}

したがって

( a 2 + b 2 ) ( ( x 0 − m ) 2 + ( y 0 − n ) 2 ) = ( a x 0 + b y 0 + c ) 2 , {\displaystyle (a^{2}+b^{2})((x_{0}-m)^{2}+(y_{0}-n)^{2})=(ax_{0}+by_{0}+c)^{2},}

となり、点(m, n)と点(x0, y0)を結ぶ線分の距離を求めることができた：

d = ( x 0 − m ) 2 + ( y 0 − n ) 2 = | a x 0 + b y 0 + c | a 2 + b 2 {\displaystyle d={\sqrt {(x_{0}-m)^{2}+(y_{0}-n)^{2}}}={\frac {|ax_{0}+by_{0}+c|}{\sqrt {a^{2}+b^{2}}}}} [4].

幾何学的な証明

幾何学的証明の概念図

この証明も、直線が軸に水平または垂直でない場合にのみ成り立つ[5]。

点P(x0, y0)からAx + By + C =0で表される直線に垂線を下ろし、垂線の足を点Rとする。また点Pからy軸に平行な直線を引き、それと元の直線の交点を点Sとする。次に、直線上に点Tを任意にとり、直角三角形TVUを描く。但しTUを斜辺とし、残り2辺はそれぞれx軸、y軸に平行とする。さらにx軸に平行な辺TVの長さは|B|となるようにする(図参照)。こうすることで、直線の傾きが −A/B であるからy軸に平行な辺VUの長さは |A| となる。

ここで、∆PRSと∆TVUは相似である。なぜならば両者とも直角三角形であり、さらにPS と UV が平行で同位角が等しいからである[注釈 1]。したがって対応する辺の長さの比は等しいので、

| P R ¯ | | P S ¯ | = | T V ¯ | | T U ¯ | . {\displaystyle {\frac {|{\overline {PR}}|}{|{\overline {PS}}|}}={\frac {|{\overline {TV}}|}{|{\overline {TU}}|}}.}

また点Sの座標を（x0,m)とすると|PS|=|y0 − m|で、点Pと直線の距離|PR|は、

| P R ¯ | = | y 0 − m | | B | A 2 + B 2 . {\displaystyle |{\overline {PR}}|={\frac {|y_{0}-m||B|}{\sqrt {A^{2}+B^{2}}}}.}

ところで点Sは直線上の点だから、mの値はA, B, Cを用いて

m = − A x 0 − C B , {\displaystyle m={\frac {-Ax_{0}-C}{B}},}

と表せるので、これを代入すれば結局[6]:

| P R ¯ | = | A x 0 + B y 0 + C | A 2 + B 2 . {\displaystyle |{\overline {PR}}|={\frac {|Ax_{0}+By_{0}+C|}{\sqrt {A^{2}+B^{2}}}}.}

なお、類似の証明として、点Vを点Pと同一の点とし、∆UVTの面積を2通りの方法で求めることにより点Pと直線の距離の公式を導く方法がある。点Vと点Pを同一の点とした時、∆UVTの面積はまず　で求められる。一方で、TUを底辺と考えることで、点Pから直線におろした垂線の長さを高さとして面積を求められる。TU, VU, VTの長さは点Pの座標と直線の方程式の係数を用いて表せるので、そこから点と直線の距離の公式が導ける[要出典]。

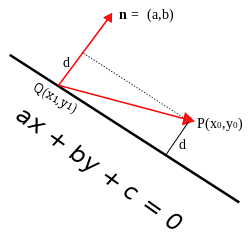
ベクトルの射影を用いた証明

図のベクター投影証
図のベクター投影証

点P(x0, y0)と、ax + by + c =0で与えられる直線を考える。また、点Q(x1, y1)を直線上の任意の点とし、ベクトルn(a, b)を点Qを始点とする法線ベクトルとする。このとき、点Pと直線の距離dは、ベクトルQPをnに直交射影したものの長さと等しい。この射影したベクトルの長さは、

d = | Q P → ⋅ n | ‖ n ‖ . {\displaystyle d={\frac {|{\overrightarrow {QP}}\cdot \mathbf {n} |}{\|\mathbf {n} \|}}.}

となる。いま、

Q P → = ( x 0 − x 1 , y 0 − y 1 ) , {\displaystyle {\overrightarrow {QP}}=(x_{0}-x_{1},y_{0}-y_{1}),}

なので、

Q P → ⋅ n = a ( x 0 − x 1 ) + b ( y 0 − y 1 ) {\displaystyle {\overrightarrow {QP}}\cdot \mathbf {n} =a(x_{0}-x_{1})+b(y_{0}-y_{1})} , ‖ n ‖ = a 2 + b 2 , {\displaystyle \|\mathbf {n} \|={\sqrt {a^{2}+b^{2}}},}

であるから、

d = | a ( x 0 − x 1 ) + b ( y 0 − y 1 ) | a 2 + b 2 . {\displaystyle d={\frac {|a(x_{0}-x_{1})+b(y_{0}-y_{1})|}{\sqrt {a^{2}+b^{2}}}}.}

点Qが直線上の点であることと c = − a x 1 − b y 1 {\displaystyle c=-ax_{1}-by_{1}} から[7]、

d = | a x 0 + b y 0 + c | a 2 + b 2 . {\displaystyle d={\frac {|ax_{0}+by_{0}+c|}{\sqrt {a^{2}+b^{2}}}}.}

その他の公式

点と直線の最短距離を表す公式は他にも考えられる。以下の導出は、やはり直線がx軸にもy軸にも平行でないことを必要とする。

点P(x0, y0)と方程式 y = m x + k {\displaystyle y=mx+k} で与えられる直線を考える。すると、点Pを通る法線の方程式は y = x 0 − x m + y 0 {\displaystyle y={\frac {x_{0}-x}{m}}+y_{0}} となる。

この2直線の交点は、直線上の点の中で点Pから最も近い点である。したがって、

m x + k = x 0 − x m + y 0 . {\displaystyle mx+k={\frac {x_{0}-x}{m}}+y_{0}.}

これをxについて解けば、

x = x 0 + m y 0 − m k m 2 + 1 . {\displaystyle x={\frac {x_{0}+my_{0}-mk}{m^{2}+1}}.}

交点のy座標は、いま得られたx座標の式を直線の方程式に代入すれば求められて、

y = m ( x 0 + m y 0 − m k ) m 2 + 1 + k . {\displaystyle y=m{\frac {(x_{0}+my_{0}-mk)}{m^{2}+1}}+k.}

2点間の距離は d = ( X 2 − X 1 ) 2 + ( Y 2 − Y 1 ) 2 {\displaystyle d={\sqrt {(X_{2}-X_{1})^{2}+(Y_{2}-Y_{1})^{2}}}} で求められるから、ここから点と直線の距離の公式として以下を得る。

d = ( x 0 + m y 0 − m k m 2 + 1 − x 0 ) 2 + ( m x 0 + m y 0 − m k m 2 + 1 + k − y 0 ) 2 = | k + m x 0 − y 0 | 1 + m 2 . {\displaystyle d={\sqrt {\left({{\frac {x_{0}+my_{0}-mk}{m^{2}+1}}-x_{0}}\right)^{2}+\left({m{\frac {x_{0}+my_{0}-mk}{m^{2}+1}}+k-y_{0}}\right)^{2}}}={\frac {|k+mx_{0}-y_{0}|}{\sqrt {1+m^{2}}}}.}

なお、ここでは直線の方程式をy=mx+kとしたが、ax+by+c=0と比較するとm =-a/b, k =- c/bである。これを上式に代入し整理すれば、最初に導出した点と直線の公式が確かに得られる[8]。

ベクトルを用いた公式

ベクトルを用いた公式の図解

直線の方程式は、ベクトル方程式として与えることもできる：

x = a + t n {\displaystyle \mathbf {x} =\mathbf {a} +t\mathbf {n} }

ここで a は直線のある点を表す位置ベクトルで、 n は直線の方向を表す単位ベクトル である。またtはスカラー変数で、xが直線の軌跡となる。

ここで、平面の任意の点 pとこの直線の距離は以下のように与えられる：

distance ⁡ ( x = a + t n , p ) = ‖ ( a − p ) − ( ( a − p ) ⋅ n ) n ‖ . {\displaystyle \operatorname {distance} (\mathbf {x} =\mathbf {a} +t\mathbf {n} ,\mathbf {p} )=\|(\mathbf {a} -\mathbf {p} )-((\mathbf {a} -\mathbf {p} )\cdot \mathbf {n} )\mathbf {n} \|.}

この公式は次のように導出できる: a − p {\displaystyle \mathbf {a} -\mathbf {p} } は点pから点aへのベクトルである。 ( a − p ) ⋅ n {\displaystyle (\mathbf {a} -\mathbf {p} )\cdot \mathbf {n} }  はそのベクトルを直線に射影したものの長さなので、

( ( a − p ) ⋅ n ) n {\displaystyle ((\mathbf {a} -\mathbf {p} )\cdot \mathbf {n} )\mathbf {n} }

は、 a − p {\displaystyle \mathbf {a} -\mathbf {p} } を直線に正射影したベクトルである。したがって、

( a − p ) − ( ( a − p ) ⋅ n ) n {\displaystyle (\mathbf {a} -\mathbf {p} )-((\mathbf {a} -\mathbf {p} )\cdot \mathbf {n} )\mathbf {n} }

は、直線に垂直な a − p {\displaystyle \mathbf {a} -\mathbf {p} } の成分である。つまり点と直線の距離は、このベクトルのノルムそのものである[9]。この公式は、二次元に限らず適用できるように一般化できる。

その他のベクトルを用いた公式

もしベクトル空間が正規直交系ならば、方向ベクトル u → {\displaystyle {\vec {u}}} を持ち点Aを通る直線lを考えると点Pと直線lの距離は、

d ( P , l ) = ‖ A P → × u → ‖ ‖ u → ‖ {\displaystyle d(\mathrm {P} ,l)={\frac {\left\|{\overrightarrow {\mathrm {AP} }}\times {\vec {u}}\right\|}{\|{\vec {u}}\|}}}

ここで A P → × u → {\displaystyle {\overrightarrow {\mathrm {AP} }}\times {\vec {u}}}  はベクトル A P → {\displaystyle {\overrightarrow {\mathrm {AP} }}} と u → {\displaystyle {\vec {u}}} の外積で、 ‖ u → ‖ {\displaystyle \|{\vec {u}}\|} は u → {\displaystyle {\vec {u}}} のノルムである。

但し、外積が存在するのは3次元と7次元の場合に限ることに注意せねばならない。

注釈

  1. ^ もし2つの三角形が直線を挟んで両側に位置した場合、この2角の関係は錯角であるからやはり等しい。

出典

  1. ^ Larson & Hostetler 2007, p. 452
  2. ^ Spain 2007
  3. ^ Larson & Hostetler 2007, p. 522
  4. ^ Laudański 2013
  5. ^ Ballantine & Jerbert 1952 なおこの制約は記事中では言及されていない
  6. ^ Ballantine & Jerbert 1952
  7. ^ Anton 1994, pp. 138–139
  8. ^ Larson & Hostetler 2007, p. 522
  9. ^ Sunday, Dan. “Lines and Distance of a Point to a Line”. softSurfer. 2013年12月6日閲覧。

参考文献

  • Anton, Howard (1994), Elementary Linear Algebra (7th ed.), John Wiley & Sons, ISBN 0-471-58742-7 
  • Ballantine, J.P.; Jerbert, A.R. (1952), “Distance from a line or plane to a point”, American Mathematical Monthly 59: 242–243, doi:10.2307/2306514 
  • Larson, Ron; Hostetler, Robert (2007), Precalculus: A Concise Course, Houghton Mifflin Co., ISBN 0-618-62719-7 
  • Spain, Barry (2007) [1957], Analytical Conics, Dover Publications, ISBN 0-486-45773-7 
  • Laudański, Ludomir (2013), Between Certainty and Uncertainty, Intelligent Systems Reference Library, Springer-Verlag Berlin Heidelberg, ISBN 978-3-642-25696-7 

関連項目

  • ヘッセ標準形
  • 2直線の交点（英語版）
  • 直線と直線の距離（英語版）
  • 点と平面の距離（英語版）
  • 英:ねじれの位置#距離

外部リンク

  • 『点と直線の距離公式：例題と4通りの証明』 - 高校数学の美しい物語
  • Deza, Michel Marie; Deza, Elena (2013), Encyclopedia of Distances (2nd ed.), Springer, p. 86, ISBN 9783642309588, https://books.google.com/books?id=QxX2CX5OVMsC&pg=PA86