グモウスキー・ミラの写像

グモウスキー・ミラの写像のストレンジアトラクタの一例。ミラはこのアトラクタを「神話の鳥」と命名した。

グモウスキー・ミラの写像（グモウスキー・ミラのしゃぞう）は、イーゴリ・グモウスキー[1] (Igor Gumowski) とクリスチャン・ミラ (Christian Mira) によって発表された非線形の2次元離散力学系である。加速器と蓄積リングにおける不安定性の研究を出自とする。相平面上に多様な形のストレンジアトラクタが現れることで知られる。

写像

離散力学系とは、n を整数の時間として、n 番目の状態 xn がその手前の n−1 番目の状態 xn−1 によって一意に決まる法則が与えられた系である[2]。二次元の系とは、x と y の組 (x, y) = x を一つの状態とする系である。xn とxn+1 の関係を定めた関数を、力学系の話の中では単に写像ともいう[3]。グモウスキー・ミラの写像として紹介される写像はまちまちだが、次の2つの形の写像 f1 と f2 がグモウスキーとミラによって発表されたものである[4]。

f 1 = { x n + 1 = y n + g ( x n ) y n + 1 = − x n + g ( x n + 1 ) {\displaystyle f_{1}={\begin{cases}x_{n+1}=y_{n}+g(x_{n})\\y_{n+1}=-x_{n}+g(x_{n+1})\end{cases}}}
f 2 = { x n + 1 = y n + α y n ( 1 − σ y n 2 ) + g ( x n ) y n + 1 = − x n + g ( x n + 1 ) {\displaystyle f_{2}={\begin{cases}x_{n+1}=y_{n}+\alpha y_{n}(1-\sigma y_{n}^{2})+g(x_{n})\\y_{n+1}=-x_{n}+g(x_{n+1})\end{cases}}}

α と σ はパラメータ（定数係数）である。写像 f1 のヤコビアンは 1 で保存系に相当する。f2 では αyn(1 − σyn) という項が追加されており、これが減衰を発揮し、f2 は散逸系に相当する。α が小さければ、保存系に近い準保存系といえる[4]。

g(x) はグモウスキーとミラが「有界非線形性 (bounded nonlinerity)」と呼んだ項で、次の2つの形で与えた[5]。

g 1 ( x ) = μ x + 2 ( 1 − μ ) x 2 1 + x 2 {\displaystyle g_{1}(x)=\mu x+{\frac {2(1-\mu )x^{2}}{1+x^{2}}}}
g 2 ( x ) = μ x + ( 1 − μ ) x 2 exp ⁡ ( 1 − x 2 4 ) {\displaystyle g_{2}(x)=\mu x+(1-\mu )x^{2}\exp({\frac {1-x^{2}}{4}})}

μ はパラメータで、グモウスキーとミラは −1 ≤ μ ≤ 1 の範囲で与えた。 μ の値が 1 より小さくなるほど写像の非線形性が強くなる[5]。

特に、f2 と g1 が組み合わされた

{ x n + 1 = y n + α y n ( 1 − σ y n 2 ) + μ x n + 2 ( 1 − μ ) x n 2 1 + x n 2 y n + 1 = − x n + μ x n + 1 + 2 ( 1 − μ ) x n + 1 2 1 + x n + 1 2 {\displaystyle {\begin{cases}x_{n+1}=y_{n}+\alpha y_{n}(1-\sigma y_{n}^{2})+\mu x_{n}+{\dfrac {2(1-\mu )x_{n}^{2}}{1+x_{n}^{2}}}\\y_{n+1}=-x_{n}+\mu x_{n+1}+{\dfrac {2(1-\mu )x_{n+1}^{2}}{1+x_{n+1}^{2}}}\end{cases}}}

という形の写像が「グモウスキー・ミラの写像」として紹介されることが多い[6][7][8][9][10]。

グモウスキーは1960年代から70年代にかけてジュネーブの欧州原子核研究機構で、加速器と蓄積リングにおける不安定性を研究していた。加速器あるいは蓄積リング内での粒子の横方向の運動を表現するためのモデルとして、グモウスキーとミラは保存系の写像 f1 ならびに非線形項 g1 と g2 を導入した[5]。準保存系 f2 とともに、グモウスキーとミラの1980年の著作にてこれらの写像とその計算結果が記された[4]。

軌道、アトラクタ

ストレンジアトラクタ（黒いプロット点）とそこへ吸引されるある一つの軌道（赤いプロット点と補助矢印）の様子。軌道は回転しながらストレンジアトラクタの領域に収束する。

適当な初期条件 x0 = (x0, y0) を与え、写像を繰り返し適用することで離散力学系は (x0, x1, x2,...)という軌道を作る[3]。軌道は相平面（x-y平面）上で点列となる。グモウスキー・ミラの写像はあるパラメータ範囲でストレンジアトラクタを持っている[5]。周りの軌道を吸引する部分空間があり、その部分空間上で軌道は非周期で初期値に鋭敏な点列である。一方で、その部分空間自体は不変で一定の形状を有している。このような部分空間をストレンジアトラクタと呼ぶ[11]。

グモウスキー・ミラの写像は多種多様な形状のストレンジアトラクタが現れることで知られる[6][8]。グモウスキー・ミラの写像は美的な創作にも利用されてきた[12]。特に、f2 と g1 から成る写像における鳥の羽のようなアトラクタは有名で、パラメータ (α, σ, μ) が (0.008, 0.05, −0.496) のときには3枚羽の翼が、 (0.009, 0.05, −0.801)[13] のときには5枚羽の翼が描かれる[9][14]。ミラはこれらを「神話の鳥 (mythic bird)」と名付けた[14][12]。

パラメータの値によってはストレンジアトラクタ以外のアトラクタも現れ、安定な周期点のアトラクタも現れる[6]。パラメータの値に応じて解の振る舞いが定性的に変化することを力学系では分岐と呼ぶ[2]。グモウスキー・ミラの写像は μ に対して鋭敏に反応して分岐する傾向を持つ[6]。下記に、散逸系のグモウスキー・ミラの写像（f2 ）の軌道（アトラクタ）と、保存系のグモウスキー・ミラの写像（f1 ）の軌道の例を示す。

  • 散逸系のグモウスキー・ミラの写像のアトラクタ
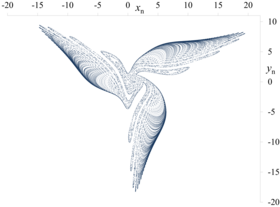  • f2-g1, α = 0.008, σ = 0.05, μ = −0.496
    f2-g1, α = 0.008, σ = 0.05, μ = −0.496
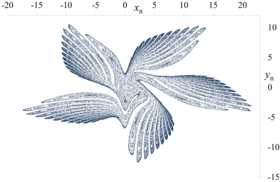  • f2-g1, α = 0.009, σ = 0.05, μ = −0.801
    f2-g1, α = 0.009, σ = 0.05, μ = −0.801
  • f2-g1, α = 0.005, σ = 0.05, μ = −0.5 （3個の周期点）
    f2-g1, α = 0.005, σ = 0.05, μ = −0.5
    （3個の周期点）
  • f2-g2, α = 0.0083, σ = 0.1, μ = −0.38
    f2-g2, α = 0.0083, σ = 0.1, μ = −0.38
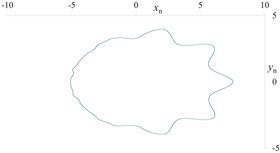  • f2-g2, α = 0.01, σ = 0.1, μ = 0.8
    f2-g2, α = 0.01, σ = 0.1, μ = 0.8
  • f2-g2, α = 0.07, σ = 0.0075, μ = −0.43 （25個の周期点）
    f2-g2, α = 0.07, σ = 0.0075, μ = −0.43
    （25個の周期点）
  • 保存系のグモウスキー・ミラの写像の軌道
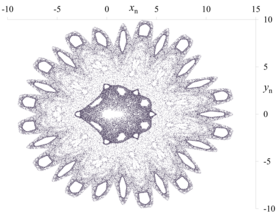  • f1-g1, μ = 0.39, x0 = 1, y0 = 1
    f1-g1, μ = 0.39, x0 = 1, y0 = 1
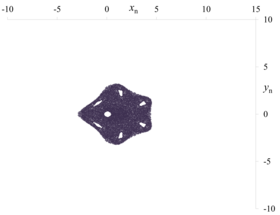  • f1-g1, μ = 0.365, x0 = 1, y0 = 1
    f1-g1, μ = 0.365, x0 = 1, y0 = 1
  • f1-g1, μ = 0.34, x0 = 1, y0 = 1
    f1-g1, μ = 0.34, x0 = 1, y0 = 1

特殊な過渡的振る舞い

アトラクタが存在する場合、軌道は十分な時間経過後にアトラクタに落ち着く。初期条件からアトラクタに引き付けられるまでの軌道を「過渡状態」などという[15]。グモウスキー・ミラの写像の振る舞いの一つとして、過渡状態の軌道がロジスティック写像の分岐図のような軌道を取ることがある[8]。ロジスティック写像は

x n + 1 = a x n ( 1 − x n ) {\displaystyle x_{n+1}=ax_{n}(1-x_{n})}

という形で与えられる1次元写像である[2]。分岐図（あるいは軌道図）はパラメータとアトラクタの様相を描くもので、ロジスティック写像の分岐図は横軸にパラメータ a を取り、縦軸に十分な時間経過後の軌道の値をプロットして描かれる[16]。相平面上の軌道とはx-y平面上に x0, x1, x2,... という点列を描くもので、分岐図とは別物である[8]。

しかし、グモウスキー・ミラの写像

{ x n + 1 = y n + α y n ( 1 − σ y n 2 ) + μ x n + 2 ( 1 − μ ) x n 2 1 + x n 2 y n + 1 = − x n + μ x n + 1 + 2 ( 1 − μ ) x n + 1 2 1 + x n + 1 2 {\displaystyle {\begin{cases}x_{n+1}=y_{n}+\alpha y_{n}(1-\sigma y_{n}^{2})+\mu x_{n}+{\dfrac {2(1-\mu )x_{n}^{2}}{1+x_{n}^{2}}}\\y_{n+1}=-x_{n}+\mu x_{n+1}+{\dfrac {2(1-\mu )x_{n+1}^{2}}{1+x_{n+1}^{2}}}\end{cases}}}

のパラメータを α = 0.008, σ = 0.05 とし、さらに μ の値を 1 よりもわずかに大きな値に選ぶとき、その軌道をx-y平面上にプロットすると、最終的に安定な3周期点に吸引されるが、そこまでの過渡状態の軌道がロジスティック写像の分岐図に非常に似た形となる[9]。

グモウスキー・ミラの写像における相平面上の軌道。パラメータは α = 0.008, σ = 0.05, μ = 1.00004 を使用。軌道は原点近傍からスタートしており、図の最右端以降では、最終的には軌道は3周期点に収束する。
ロジスティック写像の分岐図。横軸のパラメータ a が 1 から 4 までを図示している。

以上のようなことが起こるメカニズムとして、次のような説明が与えられている[9]。xn+1 対 xn、xn+1 対 yn、yn+1 対 xn、yn+1 対 yn の関係を、問題となっている領域でそれぞれ数値的に調べる。上記のようなパラメータにおいては、xn+1 の値に対して yn の変化はほとんど影響を及ぼしていない。一方、xn+1 と xn は正の傾きを持つ線形関係にある。また、yn+1 と xn も正の傾きを持つ線形関係にある。そして、yn+1 に対して yn は上に凸のグラフとなっており、単峰型の関数となっている。ロジスティック写像も単峰型の関数の形としており、問題となっている領域でグモウスキー・ミラの写像の yn+1 と yn の関係もそれと同形である。また、ロジスティック写像ではパラメータ a の値が増えるに従って単峰の最大値が徐々に大きくなる。問題となっている領域のグモウスキー・ミラの写像でも、xn の値が増えるに従って yn+1 対 yn の単峰グラフの最大値が徐々に大きくなる。したがって、問題のパラメータで相平面上に軌道を描くと、xn を少しづつ増やしながら yn の単峰関数に支配される yn+1 の終局的振る舞いを自動的に描くことなる。これは、パラメータ a を少しづつ増やしながら xn の単峰関数で与えられる xn+1 の終局的振る舞いを描くロジスティック写像分岐図の描き方と、結果的に同じである[9]。

以上のようなロジスティック写像の分岐図に似た形を持つグモウスキー・ミラの写像の過渡的振る舞いは、カオス理論の一般向け書籍の発刊過程で、出版社の担当編集者が発見した[8]。

出典

  1. ^ グモフスキーとも表記される（ミラ「グモフスキーとトゥルーズ研究グループのカオス力学前史」2002.）。
  2. ^ a b c 早間 慧、2002、『カオス力学の基礎』改訂2版、現代数学社 ISBN 4-7687-0282-1 pp. 1–7
  3. ^ a b 小室 元政、2005、『基礎からの力学系：分岐解析からカオス的遍歴へ』新版、サイエンス社〈SGC BOOKS〉 ISBN 4-7819-1118-8 pp. 22–23
  4. ^ a b c Christian Mira (2014). ABOUT WHAT IS CALLED "GUMOWSKI-MIRA MAP" (Report). ResearchGate.
  5. ^ a b c d クリスチャン・ミラ、ラルフ・エイブラハム、ヨシスケ・ウエダ（編）、稲垣 耕作・赤松 則男（訳）、2002、「グモフスキーとトゥルーズ研究グループのカオス力学前史」、『カオスはこうして発見された』初版、共立出版 ISBN 4-320-03418-X pp. 111–129
  6. ^ a b c d Ambika, K (2007). "Chapter 3: Gumowski-Mira Map". Studies on stability synchronisation and scaling behaviour in coupled non linear system (PhD thesis). Mahatma Gandhi University. pp. 61–75.
  7. ^ 高安 秀樹・本田 勝也・佐野 雅己・田崎 睛明・村山 和郎・伊藤 敬祐、2001、『フラクタル科学』初版、朝倉書店 ISBN 4-254-10063-9 pp. 74, 116
  8. ^ a b c d e 合原 一幸・黒崎 政男・高橋 純、1999、『哲学者クロサキと工学者アイハラの神はカオスに宿りたもう』初版、アスキー ISBN 4-7561-3133-6 pp. 134–135, 237–238
  9. ^ a b c d e 高橋純, 増田尚美, 山田泰司「GumowskiとMiraの写像の過渡的振舞い」『電子情報通信学会論文誌. A基礎・境界』第82巻第10号、電子情報通信学会基礎・境界ソサイエティ、1999年10月、1664-1667頁、CRID 1520853835205590400、ISSN 09135707、NAID 110003313432。 
  10. ^ 齊藤実「図形自動生成ソフトウェアの開発とその教育効果に関する一検討」『山梨学院大学経営情報学論集』第23巻、山梨学院大学経営情報学研究会、2017年3月、1-11頁、CRID 1050001337740314240、ISSN 13410806、NAID 120006243364。 
  11. ^ 井庭 崇・福原 義久、1998年、『複雑系入門―知のフロンティアへの冒険』初版、NTT出版 ISBN 4-87188-560-7 pp. 69–74
  12. ^ a b Christian Mira (2017). ARE MATHEMATICS A SOURCE OF ARTISTIC CREATION? INCURSION INTO MAPS PROPERTIES (Report). ResearchGate.
  13. ^ 正確には μ は cos(4π/5) + 0.008 という値（ミラ「グモフスキーとトゥルーズ研究グループのカオス力学前史」2002. p. 127）。
  14. ^ a b 川上 博、1990、『カオスCGコレクション』初版、サイエンス社〈Information & Computing 48〉 ISBN 978-4-7819-0591-4 pp. 33, 97
  15. ^ 船越 満明、2008、『カオス』初版、朝倉書店〈シリーズ 非線形科学入門3〉 ISBN 978-4-254-11613-7 pp.83–84
  16. ^ K. T. アリグッド・T. D. サウアー・J. A. ヨーク、津田 一郎（監訳）、星野 高志・阿部 巨仁・黒田 拓・松本 和宏（訳）、2012、『カオス　第1巻　力学系入門』、丸善出版 ISBN 978-4-621-06223-4 pp. 17–19

外部リンク

  • ウィキメディア・コモンズには、グモウスキー・ミラの写像に関するカテゴリがあります。