Persamaan kuadrat
Persamaan kuadrat adalah suatu persamaanberorde dua. Bentuk umum dari persamaan kuadrat adalah
dengan cara
Huruf-huruf a, b dan c disebut sebagai koefisien: koefisien kuadrat a adalah koefisien dari , koefisien linier b adalah koefisien dari x, dan c adalah koefisien konstan atau disebut juga suku bebas.
Arti nilai a, b, dan c
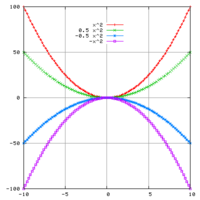 |  |  |
Nilai-nilai a, b dan c menentukan bagaimana bentuk parabola dari fungsi persamaan kuadrat dalam ruang xy.
- a menentukan seberapa cekung/cembung parabola yang dibentuk oleh fungsi kuadrat. Nilai a > 0 akan menyebabkan parabola terbuka ke atas, sedangkan nilai a < 0 akan menyebabkan parabola terbuka ke bawah.
- b menentukan kira-kira posisi x puncak parabola, atau sumbu simetri cermin dari kurva yang dibentuk. Posisi tepatnya adalah -b/2a.
- c menentukan titik potong fungsi parabola yang dibentuk dengan sumbu y atau saat x = 0.
Ilustrasi grafik-grafik persamaan kuadrat dengan berbagai variasi nilai a. b dan c dapat dilihat pada gambar diatas.
Rumus Kuadratis (Rumus abc)
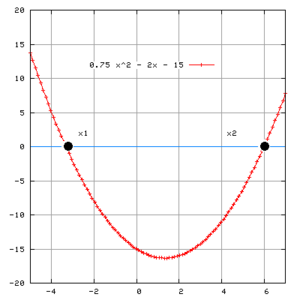
Rumus kuadratis dikenal pula dengan nama rumus abc karena digunakan untuk menghitung akar-akar persamaan kuadrat yang tergantung dari nilai-nilai a, b dan c suatu persamaan kuadrat. Rumus yang dimaksud memiliki bentuk
Rumus ini digunakan untuk mencari akar-akar persamaan kuadrat apabila dinyatakan bahwa
.
Dari rumus tersebut akan diperoleh akar-akar persamaan, sehingga persamaan semula dalam bentuk
dapat dituliskan menjadi
.
Dari persamaan terakhir ini dapat pula dituliskan dua hubungan yang telah umum dikenal, yaitu
dan
.
Ilustrasi dapat dilihat pada gambar.
- Sifat akar persamaan kuadrat
| Hubungan | Syarat |
|---|---|
| Kedua akar real tandanya positif | |
| Kedua akar real tandanya negatif | |
| Kedua akar real tandanya berlainan | |
| Kedua akar real sama | |
| Kedua akar real berkebalikan | |
| Kedua akar real berlawanan | |
| Akar tidak real (imajiner) |
Persamaan kuadrat baru
Pokok umum persamaan kuadrat baru yaitu
| Persamaan kuadrat lama | Persamaan kuadrat baru |
|---|---|
Pembuktian rumus persamaan kuadrat
Dari bentuk umum persamaan kuadrat,
bagi kedua ruas untuk mendapatkan
Pindahkan ke ruas kanan
sehingga teknik melengkapkan kuadrat bisa digunakan di ruas kiri.
Pindahkan ke ruas kanan
lalu samakan penyebut di ruas kanan.
Kedua ruas diakar (dipangkatkan setengah), sehingga tanda kuadrat di ruas kiri hilang, dan muncul tanda plus-minus di ruas kanan.
Pindahkan ke ruas kanan
sehingga didapat rumus kuadrat
- atau
Diskriminan/determinan

Dalam rumus kuadrat di atas, terdapat istilah yang berada dalam tanda akar:
yang disebut sebagai diskriminan atau juga sering disebut determinan suatu persamaan kuadrat. Kadang dinotasikan dengan huruf D.
Suatu persamaan kuadrat dengan koefisien-koefisien riil dapat memiliki hanya sebuah akar atau dua buah akar yang berbeda, di mana akar-akar yang dimaksud dapat berbentuk bilangan riil atau kompleks. Dalam hal ini diskriminan menentukan jumlah dan sifat dari akar-akar persamaan kuadrat. Terdapat tiga kasus yang mungkin:
- Jika diskriminan bersifat positif, akan terdapat dua akar berbeda yang kedua-duanya merupakan bilangan riil. Untuk persamaan kuadrat dengan koefisien berupa bilangan bulat, apabila diskriminan merupakan suatu kuadrat sempurna, maka akar-akarnya merupakan bilangan rasional—sebaliknya dapat pula merupakan bilangan irrasional kuadrat.
- Jika diskriminan bernilai nol, terdapat eksak satu akar, dan akar yang dimaksud merupakan bilangan riil. Hal ini kadang disebut sebagai akar ganda, di mana nilainya adalah:
- Jika diskriminan bernilai negatif, tidak terdapat akar riil. Sebagai gantinya, terdapat dua buah akar kompleks (tidak-real), yang satu sama lain merupakan konjugat kompleks:
dan
Jadi akar-akar akan berbeda, jika dan hanya jika diskriminan bernilai tidak sama dengan nol, dan akar-akar akan bersifat riil, jika dan hanya jika diskriminan bernilai tidak negatif.
Akar riil dan kompleks
Persamaan kuadrat dapat memiliki sebuah akar (akar ganda) atau dua buah akar yang berbeda, yang terakhir ini dapat bersifat riil atau kompleks bergantung dari nilai diskriminannya. Akar-akar persamaan kuadrat dapat pula dipandang sebagai titik potongnya dengan sumbu x atau garis y = 0.
Titik potong dengan garis y = d
Dengan cara pandang ini, rumus persamaan kuadrat dapat digunakan apabila diinginkan untuk mencari titik potong antara suatu persamaan kuadrat () dengan suatu garis mendatar (). Hal ini dapat dilakukan dengan mengurangi persamaan kuadrat tersebut dengan persamaan garis yang titik potong antar keduanya ingin dicari dan menyamakannya dengan nol.
Intepretasi yang sama pun berlaku, yaitu bila:
- diskriminan positif, terdapat dua titik potong antara dan ,
- diskriminan nol, terdapat hanya satu titik potong antara dan , dan
- diskriminan negatif, tidak terdapat titik potong antara kedua kurva, dan .
Nilai-nilai y
Akar-akar suatu persamaan kuadrat menentukan rentang x di mana nilai-nilai y berharga positif atau negatif. Harga-harga ini ditentukan oleh nilai konstanta kuadrat a:
dengan merupakan akar-akar persamaan kuadrat. Dalam tabel di atas, apabila bersifat kompleks, maka yang dimaksud adalah (nilai riil)-nya.
Geometri
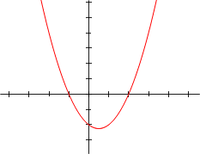
f(x) = x2 − x − 2 = (x + 1)(x − 2), dengan variabel x adalah bilangan riil. koordinat-x dari titik-titik di mana kurva menyentuh sumbu-x, x = −1 dan x = 2, adalah akar-akar dari persamaan kuadrat: x2 − x − 2 = 0.
Akar-akar dari persamaan kuadrat adalah juga pembuat nol dari fungsi kuadrat tersebut:
dikarenakan akar-akar tersebut merupakan nilai yang memberikan
Jika a, b, dan c adalah bilangan riil, dan domain dari adalah himpunan bilangan riil, maka pembuat nol dari adalah eksak koordinat-x di saat titik-titik tersebut menyentuh sumbu-x.
Mengikuti pernyataan di atas, bahwa jika diskriminan berharga positif, kurva persamaan kuadrat akan menyentuh sumbu-x pada dua buah titik (dua buah titik potong), jika berharga nol, akan menyentuh di satu titik dan jika berharga negatif, kurva tidak akan menyentuh sumbu-x.
Rumus fungsi kuadrat
Persamaan fungsi kuadrat: dimana f(x) = y maka titik balik (harga ekstrem/titik puncak) fungsi kuadrat adalah (, ).
- Pembuktian
Dari bentuk umum persamaan kuadrat,
anggapan bahwa adalah 0 maka:
- atau
maka titik balik adalah (, ).
Topik lanjutan
Metode alternatif penghitungan akar
Rumus Vieta

Rumus Vieta memberikan hubungan sederhana antara akar polinomial dan koefisiennya. Dalam kasus polinomial kuadrat, mereka mengambil bentuk berikut:
dan
Hasil ini langsung mengikuti dari relasi:
yang dapat dibandingkan istilah demi istilah dengan
Rumus pertama di atas menghasilkan ekspresi yang sesuai saat membuat grafik fungsi kuadrat. Karena grafiknya simetris terhadap garis vertikal melalui simpul, ketika ada dua akar nyata, koordinat x titik koordinat terletak di av. Jadi x koordinat dari simpul diberikan oleh ekspresi
y koordinat dapat diperoleh dengan mensubstitusi hasil di atas ke dalam persamaan kuadrat yang diberikan, memberikan
Sebagai masalah praktis, rumus Vieta menyediakan metode yang berguna untuk menemukan akar kuadrat dalam kasus di mana satu akar jauh lebih kecil dari yang lain. Bila | x 2| << | x 1|, maka x 1 + x 2 ≈ x 1, dan kami memiliki perkiraan:
Rumus Vieta kedua kemudian memberikan:
Rumus-rumus ini jauh lebih mudah untuk dievaluasi daripada rumus kuadrat dengan syarat satu akar besar dan satu akar kecil, karena rumus kuadrat mengevaluasi akar kecil sebagai selisih b), yang menyebabkan kesalahan pembulatan dalam evaluasi numerik. Gambar 5 menunjukkan perbedaan antara (i) evaluasi langsung menggunakan rumus kuadrat (akurat ketika akar memiliki nilai yang berdekatan) dan (ii) evaluasi berdasarkan perkiraan rumus Vieta di atas (akurat ketika akar berjarak lebar). Sebagai koefisien linear b meningkat, awalnya rumus kuadrat akurat, dan rumus perkiraan meningkatkan keakuratannya, yang mengarah ke perbedaan yang lebih kecil antara metode sebagai b meningkat. Namun, pada titik tertentu rumus kuadrat mulai kehilangan akurasinya karena kesalahan pembulatan, sedangkan metode perkiraan terus ditingkatkan. Akibatnya, perbedaan antara metode-metode tersebut mulai meningkat karena rumus kuadrat menjadi semakin buruk.
Situasi ini umumnya muncul dalam desain amplifier, di mana akar yang terpisah jauh diinginkan untuk memastikan operasi yang stabil (lihat respons langkah).
Solusi trigonometri
Pada hari-hari sebelum kalkulator, orang akan menggunakan tabel matematika daftar angka yang menunjukkan hasil kalkulasi dengan berbagai argumen untuk menyederhanakan dan mempercepat. Tabel logaritma dan fungsi trigonometri biasa ditemukan dalam buku teks matematika dan sains. Tabel khusus diterbitkan untuk aplikasi seperti astronomi, navigasi angkasa, dan statistik. Ada metode perkiraan numerik, yang disebut prosthaphaeresis, yang menawarkan jalan pintas di sekitar operasi yang memakan waktu seperti perkalian dan pengambilan kekuatan dan akar.[1] Para astronom, khususnya, prihatin dengan metode yang dapat mempercepat rangkaian panjang penghitungan yang terlibat dalam penghitungan mekanika angkasa.
Dalam konteks inilah kita dapat memahami perkembangan cara memecahkan persamaan kuadrat dengan bantuan substitusi trigonometri. Pertimbangkan bentuk alternatif kuadrat berikut,
[1]
dimana lambang ± dipilih sehingga a dengan c mungkin keduanya positif. Dengan mengganti
[2]
dan kemudian mengalikannya dengan cos2θ, kami dapatkan
[3]
Memperkenalkan fungsi 2θ dan mengatur ulang, kami dapatkan
[4]
[5]
Dimana tulisan di bawah garis n and p sesuai, masing-masing, dengan penggunaan tanda negatif atau positif dalam persamaan [1]. Mengganti nilai dua θn atau θp ditemukan dari persamaan [4] atau [5] menjadi [2] memberikan akar yang dibutuhkan [1]. Akar kompleks terjadi dalam solusi berdasarkan persamaan [5] bila nilai absolut sin 2θp melebihi persatuan. Jumlah upaya yang terlibat dalam menyelesaikan persamaan kuadrat menggunakan strategi pencarian tabel trigonometri dan logaritmik campuran ini adalah dua pertiga dari upaya menggunakan tabel logaritmik juga..[2] Menghitung akar kompleks akan membutuhkan penggunaan bentuk trigonometri yang berbeda.[3]
- Untuk mengilustrasikan, mari kita asumsikan bahwa kita memiliki tabel logaritma tujuh tempat dan tabel trigonometri yang tersedia, dan ingin menyelesaikan hal-hal berikut ini untuk akurasi enam angka penting:
- Tabel pemeta tujuh tempat mungkin hanya memiliki 100.000 entri, dan menghitung hasil antara ke tujuh tempat umumnya akan memerlukan interpolasi antara entri yang berdekatan.
- (dibulatkan menjadi enam angka penting)
Solusi untuk akar kompleks di koordinat polar
Jika persamaan kuadrat dengan koefisien nyata memiliki dua akar kompleks dalam kasus di mana membutuhkan a dan c untuk memiliki tanda yang sama pada solusi untuk akar dapat diekspresikan dalam bentuk polar sebagai[4]
dimana and
Solusi geometris
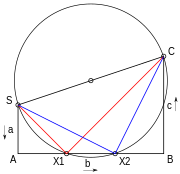
Persamaan kuadrat dapat diselesaikan secara geometris dengan beberapa cara. Salah satunya adalah melalui metode Lill. Tiga koefisien a, b, c digambar dengan sudut siku-siku antara keduanya seperti pada SA, AB, dan BC pada Gambar 6. Sebuah lingkaran digambar dengan titik awal dan akhir SC sebagai diameter. Jika ini memotong garis tengah AB dari ketiganya maka persamaan tersebut memiliki solusi, dan solusi diberikan dengan jarak negatif sepanjang garis ini dari A dibagi dengan koefisien pertama a atau SA. Bila a ialah 1 koefisien dapat dibaca secara langsung. Jadi solusi dalam diagram adalah −AX1/SA dan −AX2/SA.[5]

Lingkaran Carlyle, dinamai Thomas Carlyle, memiliki sifat bahwa solusi dari persamaan kuadrat adalah koordinat horizontal dari perpotongan lingkaran dengan horizontal.[6] Lingkaran Carlyle telah digunakan untuk mengembangkan konstruksi penggaris-dan-kompas dari poligon beraturan.
Lihat pula
- Memecahkan persamaan kuadrat dengan pecahan lanjutan
- Persamaan linier
- Fungsi kubik
- Persamaan kuartik
- Persamaan kuintik
- Teorema dasar aljabar
Referensi
- ^ Ballew, Pat. "Memecahkan Persamaan Kuadrat - Dengan metode analitik dan grafik; Termasuk beberapa metode yang mungkin belum pernah Anda lihat" (PDF). Diarsipkan dari versi asli (PDF) tanggal 9 April 2011. Diakses tanggal 18 April 2013. Parameter
|url-status=yang tidak diketahui akan diabaikan (bantuan) - ^ Seares, F. H. (1945). "Solusi Trigonometri dari Persamaan Kuadrat". Publikasi Astronomical Society of the Pacific. 57 (339): 307–309. Bibcode:1945PASP...57..307S. doi:10.1086/125759
 .
. - ^ Aude, H. T. R. (1938). "Solusi dari Persamaan Kuadrat yang Diperoleh dengan Bantuan Trigonometri". National Mathematics Magazine. 13 (3): 118–121. doi:10.2307/3028750. JSTOR 3028750.
- ^ Simons, Stuart, "Pendekatan alternatif untuk akar kompleks dari persamaan kuadrat nyata", Mathematical Gazette 93, Maret 2009, 91–92.
- ^ Bixby, William Herbert (1879), Metode Grafis untuk menemukan dengan mudah Akar Real dari Persamaan Numerik Derajat Apa Pun, West Point N. Y.
- ^ Weisstein, Eric W. "Lingkaran Carlyle". From MathWorld—A Wolfram Web Resource. Diakses tanggal 21 Mei 2013.
Bacaan lebih lanjut
- Kurnianingsih, Sri (2007). Matematika SMA dan MA 1A Untuk Kelas X Semester 1. Jakarta: Esis/Erlangga. ISBN 979-734-500-9. Parameter
|coauthors=yang tidak diketahui mengabaikan (|author=yang disarankan) (bantuan) (Indonesia) - Junaidi, Syamsul (2004). Matematika SMP Untuk Kelas IX. Jakarta: Esis/Erlangga. ISBN 979-308-232-1. Parameter
|coauthors=yang tidak diketahui mengabaikan (|author=yang disarankan) (bantuan) (Indonesia)
Pranala luar
Persamaan kuadrat
- (Indonesia) Program untuk Mencari Akar Persamaan Kuadrat.
- (Indonesia) Menyelesaikan persamaan kuadrat Diarsipkan 2008-04-30 di Wayback Machine..
- (Indonesia) Penentuan akar persamaan kuadrat (root finding) Diarsipkan 2007-01-09 di Wayback Machine.. Di sini metode pencarian akar untuk fungsi yang lebih umum, bukan hanya persamaan kuadrat.
- (Indonesia) Menyusun persamaan kuadrat Diarsipkan 2006-10-12 di Wayback Machine..
- (Indonesia) Contoh program Java menyelesaiakan persamaan kuadrat Diarsipkan 2006-07-21 di Wayback Machine.. Lihat bagian Langkah.
- (Indonesia) Saol latihan persamaan kuadrat.
- (Inggris) QuadraticEquation.
- (Inggris) Quadratic equation solver, plus solvers for cubic and quartic equations.
- (Inggris) Quadratic equation solver.
- (Inggris) Solve quadratic equations, see work shown and draw graphs.
- (Inggris) 101 uses of a quadratic equation part I Diarsipkan 2007-11-10 di Wayback Machine. Part II Diarsipkan 2007-10-22 di Wayback Machine..
- (Inggris) Quadratic graphical explorer Applet interaktif. Ubah-ubah nilai a, b, c untuk melihat efeknya pada sebuah grafik.
- (Inggris) Kode FORTRAN untuk menyelesaikan persamaan kuadrat Diarsipkan 2006-11-17 di Wayback Machine..
Pertidaksamaan kuadrat
- (Indonesia) Jenis-jenis pertidaksamaan Diarsipkan 2007-11-18 di Wayback Machine.
- (Indonesia) Aplikasi sederhana untuk memahami pertidaksamaan kuadrat Diarsipkan 2007-11-17 di Wayback Machine.






























































































































