Normaali (matematiikka)

Normaali on geometriassa vektori tai suora, joka leikkaa tasossa kohtisuorasti toista janaa, suoraa, vektoria tai käyrää vasten, taikka tilassa myös tasoa tai pintaa vasten. Tasogeometriassa suoran, janan tai vektorin normaali on toinen suora tai vektori, joka on kohtisuorassa tätä vasten. Jos kohteena on mutkitteleva käyrä, on normaali kohtisuorassa tässä kohdassa olevaa käyrän tangenttia vasten. Avaruusgeometriassa suorien, janojen ja vektorien normaali määritellään samoin kuin tasogeometriassa. Tilassa voi vielä esiintyä tasoja, joiden normaali on suora tai vektori, joka on kohtisuorassa tasoa vastaan katsottiinpa sitä tasossa miltä suunnalta hyvänsä. Tällöin normaali on kohtisuorassa tasoa vastaan. Tila-avaruudessa mutkittelevan pinnan normaali on kohtisuorassa pinnan tangenttitasoa vasten.^[1][2][3][4]

Kuvioissa kahden kohtisuorasti kohtaavan objektin väliin piirretään pieni neliö taikka kulmakaari, jonka sisälle merkitään piste. Tekstissä kohtisuoruus voidaan esittää objektien tunnusten väliin sijoitettavalla kohtisuoruussymbolilla. Seuraavassa esimerkissä ${\displaystyle a}$ ja ${\displaystyle b}$ ovat suoria, ${\displaystyle {\bar {v}}}$ ja ${\displaystyle {\bar {u}}}$ vektoreita, ${\displaystyle AB}$ ja ${\displaystyle AC}$ janoja, ${\displaystyle f}$ on käyrä, ${\displaystyle T}$ on taso ja ${\displaystyle P}$ on pinta. Silloin voidaan edellisen esityksen mukaisesti merkitä esimerkiksi

${\displaystyle a\perp b,{\bar {v}}\perp {\bar {u}},a\perp {\bar {v}},AB\perp AC,a\perp AB,a\perp f,{\bar {v}}\perp f}$

tai avaruusgeometriassa edellisten lisäksi myös vektorin kanssa esitettynä

${\displaystyle {\bar {v}}\perp f,{\bar {v}}\perp T,{\bar {v}}\perp P}$ ^[5]

ja janalla ja suoralla vastaavalla tavalla.

Tasogeometriassa

Suorat ja janat

Kahden suoran leikatessa toisensa kohtisuorasti, ovat molemmat suorat toistensa normaaleja.^[6] Koska suorien leikkauskohdassa olevat neljä kulmaa ovat toisilleen vieruskulmat ja ristikulmat, ovat ne kaikki 90°.^[7][8][1]

Normaalit voidaan aina piirtää käyttäen konstruktiivista menetelmää viivaimella ja harpilla.^[5][9] Jos tasolta, jossa kulkee jo suora, osoitetaan piste, voidaan tämän pisteen kautta aina piirtää suoralle normaali. Jos piste on annetulla suoralla, piirretään harpilla pisteen ympärille ensin ympyrä. Ympyrän ja suoran leikkauspisteistä piirretään ympyrän halkaisijan pituisella säteellä kaksi puoliympyrää niin, että nämä leikkaavat toisensa. Puoliympyröiden leikkauspisteistä vedetään suoralle normaali. Sama voidaan tehdä myös silloin, kun piste sijaitsee sivussa annetusta suorasta. Ensin piirretään riittävän pitkällä säteellä harpin avulla kaari, joka leikkaa suoraa kahdessa leikkauspisteessä. Leikkauspisteistä piirretään leikkauspisteiden välin pituisella säteellä kaksi puoliympyrän kaarta, joiden leikkauspisteiden kautta vedetään suoralle normaali.^[1]

Kahden suoran avulla, jotka leikkaavat toisensa muuten kuin kohtisuorasti, voidaan muodostaa uudet suorat, jotka ovat kohtisuorat. Koska ristikulmien kulmanpuolittajat muodostavat aina yhteisen suoran, voidaan kahden leikkaavan suoran molemmista ristikulmaparista muodostaa kaksi keskenään leikkaavaa suoraa. Näiden kulmanpuolittajasuorien välinen kulma on suorakulma, koska vieruskulmiensa (α + β = 180°) puolikkaina ne muodostavat välillensä suoran kulman (α/2 + β/2 = (α + β)/2 = 90°).^[1]

• 
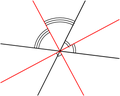  Kahden suoran muodostamien neljän kulman puolittajat leikkaavat toisensa suorassa kulmassa.
• 
  Suoralle voidaan konstruoida normaali pisteen C kautta.
• 
  Janan keskinormaalin konstruoiminen harpilla ja viivaimella.
• 
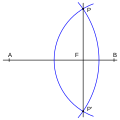  Janan normaalin konstruoiminen pisteen P kautta harpilla ja viivaimella.
• 
  Kolmion korkeusjanat ovat kohtisuorassa kolmion sivuihin tai sivujen jatkeisiin nähden.

Janalle voidaan konstruoida normaali vastaavalla tavalla. Lähtien ulkopuolisesta tai janalla olevasta pisteestä, voidaan määrätä normaali samalla tavalla. Jos jana on lyhyt, voidaan sitä aina jatkaa viivaimella, jotta piirrokset ovat riittävän laajat. Janalle voidaan muodostaa myös keskinormaali, joka kulkee janan keskipisteen kautta.^[10][11][12] Janan normaalin jokaisen pisteen etäisyydet janan kummastakin päätepisteestä ovat aina samat.^[13]

Jos janana on ympyrän säde, voidaan sen kehäpisteeseen piirtää tangentti, joka on aina ympyrän säteen normaali. Kolmion korkeusjana on sen kannan normaalin suuruinen, joka piirretään kulkemaan huipun kautta.^[14][15] Suorakulmaisen kolmion kateetit ovat toisensa normaalien suuntaiset.^[16]

Analyyttinen geometria

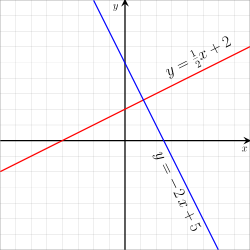
Jokaisella vaakasuoralla y = a on normaalina pystysuora x = b, joissa luvut a ja b ovat vapaasti valittavina, ja päinvastoin.^[17]

Jos annettu vinosti kulkeva suora esitetään yhtälöllä

${\displaystyle ax+by+c=0\Leftrightarrow y=-{\tfrac {a}{b}}x-{\tfrac {c}{b}}\Leftrightarrow y=kx+s}$

ja on sen kulmakerroin ${\displaystyle k=-{\tfrac {a}{b}}}$. Normaalin yhtälön kulmakertoimeksi ${\displaystyle k_{n}}$ tulee silloin

${\displaystyle k_{n}=-{\frac {1}{k}}=-(-{\frac {b}{a}})={\frac {b}{a}}.}$ ^[17]

Ehdokkaita normaaliksi on äärettömän monia, sillä suoralta on vielä valittava se piste, jonka kautta normaali kulkee. Jos valittu piste on ${\displaystyle (x_{0},y_{0})}$, saadaan yhtälöksi

${\displaystyle y-y_{0}=k_{n}(x-x_{0})\Leftrightarrow y=k_{n}x-k_{n}x_{0}+y_{0}\Leftrightarrow }$

.

${\displaystyle bx-ay+(ay_{0}-bx_{0})=0\Leftrightarrow bx-ay+d=0.}$

Vektorit

Yleisen suoran yhtälön, eli normaalimuotoisen suoran yhtälön, normaalivektori voidaan muodostaa yhtälön kertoimista

${\displaystyle ax+by+c=0\Rightarrow {\bar {n}}=a{\bar {i}}+b{\bar {j}}.}$

Merkitään vektoria ${\displaystyle {\bar {v}}=a{\bar {i}}+b{\bar {j}}={\binom {a}{b}}}$ ja ${\displaystyle {\bar {u}}=c{\bar {i}}+d{\bar {j}}={\binom {c}{d}}.}$ Vektorit ${\displaystyle {\bar {v}}}$ ja ${\displaystyle {\bar {u}}}$ ovat toistensa normaalivektoreita eli ${\displaystyle {\bar {v}}\bot {\bar {u}},}$ jos Tämä pistetulon nollasääntö on hyvä vektoreiden kohtisuoruustesti.^[17][18][7]

Funktion kuvaajan normaalit

Funktion kuvaajalle voidaan piirtää kohtaan a normaali, joka on kohtisuorassa kuvaajan samaan kohtaan piirrettyä tangenttia vastaan. Tangentin kulmakerroin ${\displaystyle k_{t}}$ kohdassa a saadaan funktion derivaatan arvosta kyseisessä kohdassa. Normaalin kulmakerroin ${\displaystyle k_{n}}$ määräytyy samalla tavalla kuin suorillakin eli

${\displaystyle k_{t}=f'(a)\Leftrightarrow k_{n}=-{\frac {1}{k_{t}}}=-{\frac {1}{f'(a)}}.}$ ^[20][21]

Normaalin yhtälö pisteessä ${\displaystyle (a,f(a)),}$ missä derivaatta on olemassa muttei ole arvoltaan nolla, on

${\displaystyle y-f(a)=-{\frac {1}{f'(a)}}(x-a).}$ ^[17][20][21]

Jos derivaattaa ei siinä kohdassa ole olemassa, on normaalin yhtälö ${\displaystyle x=f(a).}$ Jos derivaatta on nolla, tulee normaalin yhtälöksi ottaa pystysuora ${\displaystyle x=a.}$ ^[17][22]

Tason käyrät

Ympyrän normaali on säteen suuntainen, koska ympyrän tangentti on sädettä kohtisuorassa ja normaali tangenttia kohtisuorassa.^[23]

Avaruusgeometriassa

Tasot yleisesti ja analyyttisessä geometriassa

Tila-avaruudessa esitettävä taso voi olla äärettömän monessa asennossa ja kohdassa, joten tasolle voidaan asettaa normaalisuora, -jana tai -vektori äärettömän moneen kohtaan. Lukuisista sijoitusvaihtoehdoista huolimatta samalla puolella tasoa olevat normaalivektorit osoittavat aina samaan suuntaan, kun tason vastakkaisella puolella olevat normaalivektorit osoittavat vastakkaiseen suuntaan. Molemmilla vektoreilla voidaan suunnata normaalisuorat, jotka ovat keskenään yhdensuuntaiset.

Tasolle sijoitettava normaali tulee olla kohtisuorassa kaikkien tasonsuuntaisten vektorien kanssa. Riittää kuitenkin valita kaksi tasonsuuntaista vektoria (esimerkiksi ${\displaystyle {\bar {v}}}$ ja ${\displaystyle {\bar {u}}}$), jotka ovat keskenään erisuuntaiset, ja normaali ${\displaystyle {\bar {n}}}$ voidaan määrittää näiden avulla käyttäen pistetuloa

${\displaystyle {\bar {n}}\cdot {\bar {v}}={\bar {n}}\cdot {\bar {u}}=0.}$ ^[24][25]

Tason yhtälö voidaan muodostaa vektoreilla käyttäen normaalivektoria ${\displaystyle {\bar {n}}}$. Valitaan tasolta piste P, jonka avulla muut tason pisteet Q ilmoitetaan. Tasoehto sisältää pistetulon, jossa normaalivektori kerrotaan paikkavektoreiden erotuksella

${\displaystyle 0=({\bar {Q}}-{\bar {P}})\cdot {\bar {n}}={\bar {Q}}\cdot {\bar {n}}-{\bar {P}}\cdot {\bar {n}}={\begin{pmatrix}x\\y\\z\end{pmatrix}}\cdot {\begin{pmatrix}A\\B\\C\end{pmatrix}}-{\begin{pmatrix}p_{x}\\p_{y}\\p_{z}\end{pmatrix}}\cdot {\begin{pmatrix}A\\B\\C\end{pmatrix}}}$

.

${\displaystyle =Ax+By+Cz-(Ap_{x}+Bp_{y}+Cp_{z})=Ax+By+Cz+D=0.}$ ^[26]

Tason yhtälön muuttujien kertoimet A, B ja C ovat siten normaalinvektorin komponentteja.

• 
  Normaalivektorin asento lukittuu jo kahden kohtisuoruusehdon avulla. Tason ylä- ja alapuoliset vektorit ovat yhdensuuntaiset keskenään.
• 
  Tason yläpuolisesta pisteestä voidaan piirtää kohtisuora jana tasolle. Tämä on lyhin jana tasolle ja jana on silloin tason normaalin suuntainen.
• 
  Yleisen pinnan tangenttitaso määrittää yksikäsitteisesti normaalin asennon.
• 
  Yleisellä taipuisalla pinnalla jokaisessa pisteessä normaali voi olla erisuuntainen ympäristön normaaleihin verrattuna.

Yleiset pinnat

Tilassa mutkittelevan pinnan eri kohtien tangenttitasot ovat eri asennoissa. Tason normaalit, jotka ovat samalla myös pinnan normaalivektorit, ovat siten myös eri asennoissa. Jos esimerkiksi kaksiulotteinen pinta P mutkittelee kolmiulotteisessa avaruudessa, voidaan se joissakin tapauksissa esittää yhtälöllä ${\displaystyle z=f(x,y).}$ Tämän pinnan normaali pisteessä ${\displaystyle (x_{0},y_{0})}$ voidaan laskea osittaisderivaatoilla

${\displaystyle {\bar {n}}={\begin{pmatrix}f_{x}(x_{0},y_{0})\\f_{y}(x_{0},y_{0})\\-1\end{pmatrix}},}$

missä ${\displaystyle f_{x}={\frac {\partial f}{\partial x}}}$ ja ${\displaystyle f_{y}={\frac {\partial f}{\partial y}}.}$ ^[25][27][28]

Vektorit

Kuten tasossakin, kaksi vektoria ${\displaystyle {\bar {v}}=a{\bar {i}}+b{\bar {j}}+c{\bar {k}}={\begin{pmatrix}a\\b\\c\end{pmatrix}}}$ ja ${\displaystyle {\bar {u}}=d{\bar {i}}+e{\bar {j}}+f{\bar {k}}={\begin{pmatrix}d\\e\\f\end{pmatrix}}}$ ovat kohtisuorassa eli ${\displaystyle {\bar {v}}\bot {\bar {u}},}$ kun

${\displaystyle {\bar {v}}\cdot {\bar {u}}={\begin{pmatrix}a\\b\\c\end{pmatrix}}\cdot {\begin{pmatrix}d\\e\\f\end{pmatrix}}=ad+be+cf=0.}$ ^[17]

Lähteet

• Väisälä, Kalle: Geometria. Porvoo: Wsoy, 1959. Teoksen verkkoversio (pdf) (viitattu 1.1.2013).
• Seppänen, Raimo et al.: MAOL. (lukion taulukkokirja). Helsinki: Otava, 2006. ISBN 951-1-20607-9.
• Harju, Tero: Geometrian lyhyt kurssi (pdf) (luentomoniste) users.utu.fi. 2012. Turun yliopisto. Viitattu 1.4.2012.
• Kurittu Lassi: Geometria (pdf) (luentomoniste) 2006. Jyväskylän: Jyväskylän Yliopisto. Viitattu 1.4.2013.

Viitteet

Kirjallisuutta

• Kivelä, Simo K.: Algebra ja geometria. Espoo: Otatieto, 1989. ISBN 951-672-103-6.