Hipótesis de Riemann

En matemáticas puras, la hipótesis de Riemann, formulada por primera vez por Bernhard Riemann en 1859, es una conjetura sobre la distribución de los ceros de la función zeta de Riemann ζ(s).^[1]​

La hipótesis de Riemann, por su relación con la distribución de los números primos en el conjunto de los naturales, es uno de los problemas abiertos más importantes en la matemática contemporánea.^[2]​ El Instituto Clay de Matemáticas ha ofrecido un premio de un millón de dólares a la primera persona que desarrolle una demostración correcta de la conjetura.^[3]​

La hipótesis de Riemann y algunas de sus generalizaciones, junto con la conjetura de Goldbach y la conjetura de los primos gemelos, constituyen el octavo problema de Hilbert en la lista de veintitrés problemas sin resolver de David Hilbert; también es uno de los Problemas del milenio del Instituto Clay de Matemáticas, que ofrece 1 millón de dólares a quien resuelva cualquiera de ellos. El nombre también se utiliza para algunos análogos estrechamente relacionados, como la hipótesis de Riemann para curvas sobre campos finitos.

Definición

La función zeta de Riemann ζ(s) está definida en los números complejos como la suma de una serie infinita de la siguiente forma:

${\displaystyle \zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}={\frac {1}{1^{s}}}+{\frac {1}{2^{s}}}+{\frac {1}{3^{s}}}+\cdots }$

y es convergente cuando la parte real es estrictamente mayor que 1. Leonhard Euler (que murió 43 años antes de que Riemann naciera) demostró que esta serie equivale al producto de Euler:

${\displaystyle \zeta (s)=\prod _{p{\text{ primo}}}{\frac {1}{1-p^{-s}}}={\frac {1}{1-2^{-s}}}\cdot {\frac {1}{1-3^{-s}}}\cdot {\frac {1}{1-5^{-s}}}\cdot {\frac {1}{1-7^{-s}}}\cdots {\frac {1}{1-p^{-s}}}\cdots }$

donde el producto infinito se extiende sobre el conjunto de todos los números primos p, y de nuevo converge para los complejos s cuya parte real sea mayor que 1. La convergencia del producto de Euler muestra que ζ(s) no tiene ceros en esta región, puesto que ninguno de los factores tiene ceros. La hipótesis de Riemann trata de los ceros fuera de la región de convergencia de la suma de la serie descrita anteriormente y del producto de Euler asociado. Para preservar el sentido de esta hipótesis es necesario prolongar analíticamente la función zeta de Riemann ζ(s) de forma que tenga sentido para cualquier valor de s. En particular se puede expresar mediante la siguiente ecuación funcional:

${\displaystyle \zeta (s)=2^{s}\pi ^{s-1}\ \operatorname {sen} \left({\frac {\pi s}{2}}\right)\ \Gamma (1-s)\ \zeta (1-s)\!}$

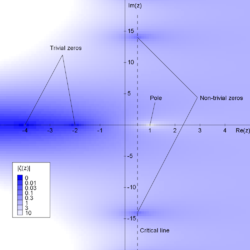
válida para todos los números complejos excepto para s = 1, donde la función tiene un polo. Como se decía anteriormente, la hipótesis de Riemann trata de los ceros de esta versión de la función zeta extendida analíticamente. Esta posee ciertos valores, llamados ceros "triviales", para los cuales la función zeta se anula. De la ecuación se puede ver que s = −2, s = −4, s = −6, ... (todos los enteros pares negativos) son ceros triviales. Así mismo, existen otros valores complejos s, que cumplen la condición 0 < Re(s) < 1, para los cuales la función zeta también se anula, son los llamados ceros "no triviales". La conjetura de Riemann hace referencia a estos ceros no triviales afirmando:

Por lo tanto los ceros no triviales deberían encontrarse en la línea crítica s = 1/2 + i t, donde t es un número real e i es la unidad imaginaria. La función zeta de Riemann, a lo largo de la línea crítica ha sido estudiada en términos de la función Z, cuyos ceros corresponden a los ceros de la función zeta sobre la línea crítica.

Entonces se puede definir ζ(s) para todos los números complejos restantes no nulos s (Re(s) ≤ 0 y s ≠ 0) aplicando esta ecuación fuera de la franja, y dejando que ζ(s) sea igual al lado derecho de la ecuación siempre que s tenga parte real no positiva (y s ≠ 0).

Si s es un entero par negativo entonces ζ(s) = 0 porque el factor sin (πs/2) desaparece; estos son los ceros triviales de la función zeta. (Si s es un entero par positivo este argumento no se aplica porque los ceros de la función seno son anulados por los polos de la función gamma ya que toma argumentos enteros negativos).

El valor ζ(0) = -1/2 no viene determinado por la ecuación funcional, sino que es el valor límite de ζ(s) a medida que s se aproxima a cero. La ecuación funcional también implica que la función zeta no tiene ceros con parte real negativa aparte de los ceros triviales, por lo que todos los ceros no triviales se encuentran en la franja crítica donde s tiene parte real entre 0 y 1.

• 
  Función zeta de Riemann a lo largo de la línea crítica con Re(s) = 1/2. Los valores reales se muestran en el eje horizontal y los valores imaginarios en el eje vertical. Re(ζ(1/2 + it)), Im(ζ(1/2 + it)) se representa con t entre -30 y 30.^[4]​
• Animación que muestra en 3D la franja crítica de la función zeta de Riemann (azul, donde s tiene parte real entre 0 y 1), la línea crítica (roja, para parte real de s igual a 0,5) y los ceros (cruce entre rojo y naranja): [x,y,z] = [Re(ζ(r + it)), Im(ζ(r + it)), t] con 0.1 ≤ r ≤ 0.9 y 1 ≤ t ≤ 51
• 
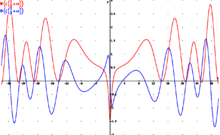
  Parte real (rojo) y parte imaginaria (azul) de la función zeta de Riemann ζ(s) a lo largo de la recta crítica en el plano complejo con parte real Re(s) = 1/2. Los primeros no triviales ceros, donde ζ(s) es igual a cero, ocurren donde ambas curvas tocan el eje horizontal x, para números complejos con partes imaginarias Im(s) iguales a ±14,135, ±21,022 y ±25,011.

Historia

"...es ist sehr wahrscheinlich, dass alle Wurzeln reell sind. Hiervon wäre allerdings ein strenger Beweis zu wünschen; ich habe indess die Aufsuchung desselben nach einigen flüchtigen vergeblichen Versuchen vorläufig bei Seite gelassen, da er für den nächsten Zweck meiner Untersuchung entbehrlich schien."

("…es muy probable que todas las raíces sean reales. Claro que uno desearía tener una demostración rigurosa; Por el momento, tras algunos intentos fugaces en vano, he pospuesto su búsqueda, ya que parece ser prescindible para lograr el objetivo inmediato de mi investigación.")

Afirmación de Riemann sobre la hipótesis de Riemann, de (Riemann, 1859). (Aquí habla de una versión de la función zeta de Riemann, modificada para que sus raíces (ceros) sean reales en vez de estar en la línea crítica.)

Riemann mencionó la conjetura en 1859, que sería llamada la hipótesis de Riemann, en su tesis de doctorado Sobre los números primos menores que una magnitud dada, al desarrollar una fórmula explícita para calcular la cantidad de primos menores que x. Puesto que no era esencial para el propósito central de su artículo, no intentó dar una demostración. Él sabía que los ceros no triviales de la función zeta están distribuidos en torno a la recta s = 1/2 + i t, y sabía también que todos los ceros no triviales debían estar en el rango 0 ≤ Re(s) ≤ 1.^[5]​

En 1896, Hadamard y de la Vallée-Poussin probaron independientemente, que ningún cero podía estar sobre la recta Re(s) = 1. Junto con las otras propiedades de los ceros no triviales demostradas por Riemann, esto mostró que todos los ceros no triviales deben estar en el interior de la banda crítica 0 < Re(s) < 1. Este fue un paso fundamental para las primeras demostraciones del teorema de los números primos.

En 1900, Hilbert incluyó la hipótesis de Riemann en su famosa lista de los 23 problemas no resueltos — es parte del problema 8 en la lista de Hilbert junto con la conjetura de Goldbach. Cuando se le preguntó qué haría si se despertara habiendo dormido quinientos años, remarcablemente Hilbert contestó que su primera pregunta sería si la hipótesis de Riemann había sido probada. La hipótesis de Riemann es el único problema de los que propuso Hilbert que está en el premio del milenio del Instituto Clay de Matemáticas.

En 1914, Hardy demostró que existe un número infinito de ceros sobre la recta crítica Re(s) = 1/2. Sin embargo todavía era posible que un número infinito (y posiblemente la mayoría) de los ceros no triviales se encontraran en algún otro lugar sobre la banda crítica. En trabajos posteriores de Hardy y Littlewood en 1921 y de Selberg en 1942 se dieron estimaciones para la densidad promedio de los ceros sobre la línea crítica.

La mayor parte de la comunidad matemática piensa que la conjetura es correcta, aunque otros grandes matemáticos como J. E. Littlewood y Atle Selberg se han mostrado escépticos, si bien el escepticismo de Selberg fue disminuyendo desde sus días de juventud. En un artículo en 1989 sugirió que un análogo debe ser cierto para una clase mucho más amplia de funciones (la clase de Selberg). Trabajos recientes se han concentrado en el cálculo explícito de la localización de grandes cantidades de ceros (con la esperanza de hallar algún contraejemplo) y en el establecimiento de cotas superiores en la proporción de ceros que puedan estar lejos de la línea crítica (con la esperanza de reducirlas a cero).

En septiembre de 2018, Michael Atiyah – laureado con la Medalla Fields (1966), entre otros galardones – presentó una fallida prueba por contradicción de la Hipótesis de Riemann en el Heidelberg Laureate Forum 2018 (Alemania)^[6]​.

La motivación original de Riemann para estudiar la función zeta y sus ceros fue su aparición en su fórmula explícita para la número de primos π(x) menor o igual que un número dado x, que publicó en su artículo de 1859 «Sobre el número de primos menores que una magnitud dada». Su fórmula se dio en términos de la función relacionada

${\displaystyle \Pi (x)=\pi (x)+{\tfrac {1}{2}}\pi (x^{1/2})+{\tfrac {1}{3}}\pi (x^{1/3})+{\tfrac {1}{4}}\pi (x^{1/4})+{\tfrac {1}{5}}\pi (x^{1/5})+{\tfrac {1}{6}}\pi (x^{1/6})+\cdots }$

que cuenta los primos y potencias de primos hasta x, contando una potencia de primo pⁿ como ¹⁄_n. El número de primos se puede recuperar a partir de esta función utilizando la fórmula de inversión de Möbius,

${\displaystyle {\begin{aligned}\pi (x)&=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n}}\Pi (x^{1/n})\\&=\Pi (x)-{\frac {1}{2}}\Pi (x^{1/2})-{\frac {1}{3}}\Pi (x^{1/3})-{\frac {1}{5}}\Pi (x^{1/5})+{\frac {1}{6}}\Pi (x^{1/6})-\cdots ,\end{aligned}}}$

donde μ es la función de Möbius. La fórmula de Riemann es entonces

${\displaystyle \Pi _{0}(x)=\operatorname {li} (x)-\sum _{\rho }\operatorname {li} (x^{\rho })-\log 2+\int _{x}^{\infty }{\frac {dt}{t(t^{2}-1)\log t}}}$

donde la suma es sobre los ceros no triviales de la función zeta y donde Π₀ es una versión ligeramente modificada de Π que sustituye su valor en sus puntos de discontinuidad por la media de sus límites superior e inferior:

${\displaystyle \Pi _{0}(x)=\lim _{\varepsilon \to 0}{\frac {\Pi (x-\varepsilon )+\Pi (x+\varepsilon )}{2}}.}$

El sumatorio de la fórmula de Riemann no es absolutamente convergente, pero puede evaluarse tomando los ceros ρ por orden del valor absoluto de su parte imaginaria. La función li que aparece en el primer término es la función integral logarítmica (no compensada) dada por el valor principal de Cauchy de la integral divergente

${\displaystyle \operatorname {li} (x)=\int _{0}^{x}{\frac {dt}{\log t}}.}$

Los términos li(x^ρ) que involucran los ceros de la función zeta necesitan cierto cuidado en su definición ya que li tiene puntos de ramificación en 0 y 1, y se definen (para x > 1) por continuación analítica en la variable compleja ρ en la región Re(ρ) > 0, es decir. es decir, deben considerarse como Ei(ρ log x). Los otros términos también corresponden a ceros: el término dominante li(x) proviene del polo en s = 1, considerado como un cero de multiplicidad -1, y los restantes términos pequeños provienen de los ceros triviales. Para algunas gráficas de las sumas de los primeros términos de esta serie véase Riesel y Göhl (1970) o Zagier (1977).

Esta fórmula dice que los ceros de la función zeta de Riemann controlan la oscilacións de los números primos alrededor de sus posiciones «esperadas». Riemann sabía que los ceros no triviales de la función zeta se distribuían simétricamente alrededor de la recta s = 1/2 + it, y sabía que todos sus ceros no triviales debían encontrarse en el intervalo 0 ≤ Re(s) ≤ 1.. Comprobó que algunos de los ceros estaban en la recta crítica con parte real 1/2 y sugirió que todos lo estaban; ésta es la hipótesis de Riemann.

El resultado ha captado la imaginación de la mayoría de los matemáticos por ser tan inesperado, ya que conecta dos áreas aparentemente no relacionadas de las matemáticas; a saber, la teoría de números, que es el estudio de lo discreto, y el análisis complejo, que se ocupa de los procesos continuos. (Burton, 2006, p. 376)

La hipótesis de Riemann y los números primos

La formulación tradicional de la hipótesis de Riemann oscurece un poco la importancia real de la conjetura. La función zeta de Riemann tiene una profunda conexión con los números primos y Helge von Koch demostró en 1901 que la hipótesis de Riemann es equivalente al considerable refinamiento del teorema de los números primos: Existe una constante C > 0 tal que

${\displaystyle \left|\pi (x)-\int _{2}^{x}{\frac {dt}{\ln(t)}}\right|\leq C\,{\sqrt {x}}\,\ln(x),}$

para todo x suficientemente grande, donde π(x) es la función contadora de primos y ln(x) es el logaritmo natural de x. Lowell Schoenfeld mostró que se puede tomar C = 1/(8 π) para todo x ≥ 2657.

Los ceros de la función zeta y los números primos satisfacen ciertas propiedades de dualidad, conocidas como fórmulas explícitas, que muestran, usando análisis de Fourier, que los ceros de la función zeta de Riemann pueden interpretarse como frecuencias armónicas en la distribución de los números primos.

Más aún, si la conjetura de Hilbert-Polya es cierta, entonces cualquier operador que nos dé las partes imaginarias de los ceros como sus valores propios debe satisfacer:

${\displaystyle \sum _{n}e^{-\beta E_{n}}=\operatorname {tr} [e^{-\beta {\hat {H}}}]=e^{u/2}-e^{-u/2}{\frac {d\psi _{0}}{du}}-{\frac {e^{u/2}}{e^{3u}-e^{u}}},}$

donde tr es la traza del operador (suma de sus valores propios), ${\displaystyle \beta \,}$ es un número imaginario y ${\displaystyle \psi (x)\,}$ es la función de Chebyshov que nos suma el log(x) sobre los primos y sus potencias enteras, dicha fórmula es una conclusión de la 'fórmula explícita' de V. Mangoldt.^[7]​ Varios operadores propuestos por C. Perelman, J. Macheca y J. García, parecen corroborar los resultados de la conjetura de Hilbert sobre el operador, reproduciendo la parte imaginaria de los ceros.

Cálculo numérico

• En el año 2004 Xavier Gourdon verificó la conjetura de Riemann numéricamente a lo largo de los primeros diez trillones de ceros no triviales de la función. Sin embargo esto no es estrictamente una demostración, numéricamente es más interesante encontrar un contraejemplo, es decir un valor de cero que no cumpla con que su parte real es 1/2, pues esto echaría por los suelos la validez de la conjetura.

• Hasta el 2005, el intento más serio para explorar los ceros de la función-ζ, es el ZetaGrid, un proyecto de computación distribuida con la capacidad de verificar billones de ceros por día. El proyecto acabó en diciembre de 2005, y ninguno de los ceros pudo ser identificado como contraejemplo de la hipótesis de Riemann.

Repercusiones de la Hipótesis de Riemann

La Hipótesis de Riemann afirma que todos los otros ceros no triviales de la función ${\displaystyle \zeta }$ (zeta) se encuentran en la recta vertical que pasa por ${\displaystyle {\frac {1}{2}}}$, es decir, son números complejos de la forma ${\displaystyle {\frac {1}{2}}+it}$, ${\displaystyle t\in \mathbb {R} }$.

Esta función tiene una profunda conexión con los números primos donde los ceros de la función zeta y los números primos satisfacen ciertas propiedades de dualidad, conocidas como fórmulas explícitas, que muestran, usando análisis de Fourier, que estos ceros pueden interpretarse como frecuencias armónicas en la distribución de los números primos.

Conociendo la relación de los números primos con la función ${\displaystyle \zeta }$, las repercusiones que tuvo esta función son algunas de estas:

• Estimadores precisos del término del resto del teorema de los números primos:

Hege von Koch demostró que la hipótesis de Riemann es equivalente al teorema de los números primos en el cual se enuncia que:

Existe una constante C tal que:

• Comparación de ${\displaystyle \pi (x)}$ y Li(x):

Para valores de x pequeños se había demostrado ${\displaystyle \pi (x)\leq \operatorname {Li} (x)}$ lo que llevó a conjeturar Li(x) era una cota superior estricta de ${\displaystyle \pi (x)}$ y por tanto la ecuación ${\displaystyle \pi (x)-\operatorname {Li} (x)}$ no tenía soluciones reales.

No obstante, en 1914 Littlewood empleó la Hipótesis de Riemann para mostrar que la desigualdad ${\displaystyle \pi (x)\leq \operatorname {Li} (x)}$ se invierte para valores suficientemente grandes de x.

En 1933 Skewes usó la Hipótesis de Reimann para mostrar que la desigualdad se invierte para algunos ${\displaystyle x<10^{10^{10^{34}}}}$y en 1955, sin usar la Hipótesis, mostró que la desigualdad se invierte para algunos ${\displaystyle x<10^{10^{10^{963}}}}$

• Las distancias entre los números primos consecutivos:

Cramér mostró que la RH implica que existe una constante ${\displaystyle C:p_{k+1}-p_{k}=C{\sqrt {p_{k}}}\log p_{k}}$ donde ${\displaystyle p_{k}}$ es el k-ésimo primo. Existe un resultado mejor que el de Cramér que es enunciado por la siguiente conjetura:

No obstante, Cramér también conjeturó que la brecha es ${\displaystyle C(\log p_{k})^{2}}$.

Véase también

• Teorema de los números primos
• Función contador de números primos
• Fórmula explícita
• Teoría analítica de números

Referencias

Bibliografía

• Artin, Emil (1924), «Quadratische Körper im Gebiete der höheren Kongruenzen. II. Analytischer Teil», Mathematische Zeitschrift 19 (1): 207-246, S2CID 117936362, doi:10.1007/BF01181075 .
• Backlund, R. J. (1914), «Sur les Zéros de la Fonction ζ(s) de Riemann», C. R. Acad. Sci. Paris 158: 1979-1981 .
• Beurling, Arne (1955), «A closure problem related to the Riemann zeta-function», Proceedings of the National Academy of Sciences of the United States of America 41 (5): 312-314, Bibcode:1955PNAS...41..312B, MR 0070655, PMC 528084, PMID 16589670, doi:10.1073/pnas.41.5.312 .
• Björner, Anders (2011), «A cell complex in number theory», Advances in Applied Mathematics 46 (1–4): 71-85, arXiv:1101.5704, doi:10.1016/j.aam.2010.09.007 .
• Bohr, H.; Landau, E. (1914), «Ein Satz über Dirichletsche Reihen mit Anwendung auf die ζ-Funktion und die L-Funktionen», Rendiconti del Circolo Matematico di Palermo 37 (1): 269-272, S2CID 121145912, doi:10.1007/BF03014823 .
• Bombieri, Enrico (2000), The Riemann Hypothesis – official problem description, Clay Mathematics Institute, archivado desde el original el 22 de diciembre de 2015, consultado el 25 de octubre de 2008 . Reprinted in (Borwein et al., 2008).
• Borwein, Peter; Choi, Stephen; Rooney, Brendan et al., eds. (2008), The Riemann Hypothesis: A Resource for the Afficionado and Virtuoso Alike, CMS Books in Mathematics, New York: Springer, ISBN 978-0-387-72125-5, doi:10.1007/978-0-387-72126-2  Se sugiere usar |número-editores= (ayuda).
• Borwein, Peter; Ferguson, Ron; Mossinghoff, Michael J. (2008), «Sign changes in sums of the Liouville function», Mathematics of Computation 77 (263): 1681-1694, Bibcode:2008MaCom..77.1681B, MR 2398787, doi:10.1090/S0025-5718-08-02036-X .
• de Branges, Louis (1992), «The convergence of Euler products», Journal of Functional Analysis 107 (1): 122-210, MR 1165869, doi:10.1016/0022-1236(92)90103-P .
• Broughan, Kevin (2017), Equivalents of the Riemann Hypothesis, Cambridge University Press, ISBN 978-1108290784 .
• Burton, David M. (2006), Elementary Number Theory, Tata McGraw-Hill Publishing Company Limited, ISBN 978-0-07-061607-3 .
• Cartier, P. (1982), «Comment l'hypothèse de Riemann ne fut pas prouvée», Seminar on Number Theory, Paris 1980–81 (Paris, 1980/1981), Progr. Math. 22, Boston, MA: Birkhäuser Boston, pp. 35-48 .
• Connes, Alain (1999), «Trace formula in noncommutative geometry and the zeros of the Riemann zeta function», Selecta Mathematica, New Series 5 (1): 29-106, MR 1694895, S2CID 55820659, arXiv:math/9811068, doi:10.1007/s000290050042 .
• Connes, Alain (2000), «Noncommutative geometry and the Riemann zeta function», Mathematics: frontiers and perspectives, Providence, R.I.: American Mathematical Society, pp. 35-54, MR 1754766 .
• Connes, Alain (2016), «An Essay on the Riemann Hypothesis», en Nash, J. F.; Rassias, Michael, eds., Open Problems in Mathematics, New York: Springer, pp. 225-257, arXiv:1509.05576, doi:10.1007/978-3-319-32162-2_5 .
• Conrey, J. B. (1989), «More than two fifths of the zeros of the Riemann zeta function are on the critical line», J. Reine Angew. Math. 1989 (399): 1-26, MR 1004130, S2CID 115910600, doi:10.1515/crll.1989.399.1 .
• Conrey, J. Brian (2003), «The Riemann Hypothesis», Notices of the American Mathematical Society: 341-353 . Reprinted in (Borwein et al., 2008).
• Conrey, J. B.; Li, Xian-Jin (2000), «A note on some positivity conditions related to zeta and L-functions», International Mathematics Research Notices 2000 (18): 929-940, MR 1792282, S2CID 14678312, arXiv:math/9812166, doi:10.1155/S1073792800000489 .
• Deligne, Pierre (1974), «La conjecture de Weil. I», Publications Mathématiques de l'IHÉS 43: 273-307, MR 0340258, S2CID 123139343, doi:10.1007/BF02684373 .
• Deligne, Pierre (1980), «La conjecture de Weil : II», Publications Mathématiques de l'IHÉS 52: 137-252, S2CID 189769469, doi:10.1007/BF02684780 .
• Deninger, Christopher (1998), «Some analogies between number theory and dynamical systems on foliated spaces», Proceedings of the International Congress of Mathematicians, Vol. I (Berlin, 1998), Documenta Mathematica, pp. 163-186, MR 1648030 .
• Dudek, Adrian W. (21 de agosto de 2014), «On the Riemann hypothesis and the difference between primes», International Journal of Number Theory 11 (3): 771-778, Bibcode:2014arXiv1402.6417D, ISSN 1793-0421, S2CID 119321107, arXiv:1402.6417, doi:10.1142/S1793042115500426 .
• Dyson, Freeman (2009), «Birds and frogs», Notices of the American Mathematical Society 56 (2): 212-223, MR 2483565 .
• Edwards, H. M. (1974), Riemann's Zeta Function, New York: Dover Publications, ISBN 978-0-486-41740-0, MR 0466039 .
• Fesenko, Ivan (2010), «Analysis on arithmetic schemes. II», Journal of K-theory 5 (3): 437-557, doi:10.1017/is010004028jkt103 .
• Ford, Kevin (2002), «Vinogradov's integral and bounds for the Riemann zeta function», Proceedings of the London Mathematical Society, Third Series 85 (3): 565-633, MR 1936814, S2CID 121144007, arXiv:1910.08209, doi:10.1112/S0024611502013655 .
• Franel, J.; Landau, E. (1924), «Les suites de Farey et le problème des nombres premiers" (Franel, 198–201); "Bemerkungen zu der vorstehenden Abhandlung von Herrn Franel (Landau, 202–206)», Göttinger Nachrichten: 198-206 .
• Ghosh, Amit (1983), «On the Riemann zeta function—mean value theorems and the distribution of |S(T)|», J. Number Theory 17: 93-102, doi:10.1016/0022-314X(83)90010-0 .
• Gourdon, Xavier (2004), The 10¹³ first zeros of the Riemann Zeta function, and zeros computation at very large height .
• Gram, J. P. (1903), «Note sur les zéros de la fonction ζ(s) de Riemann», Acta Mathematica 27: 289-304, S2CID 115327214, doi:10.1007/BF02421310 .
• Hadamard, Jacques (1896), «Sur la distribution des zéros de la fonction ζ(s) et ses conséquences arithmétiques», Bulletin de la Société Mathématique de France 14: 199-220, doi:10.24033/bsmf.545 . Reprinted in (Borwein et al., 2008).

Hanga, Catalin (2020), Random matrix models for Gram's law (phd), University of York .

• Hardy, G. H. (1914), «Sur les Zéros de la Fonction ζ(s) de Riemann», C. R. Acad. Sci. Paris 158: 1012-1014, JFM 45.0716.04 . Reprinted in (Borwein et al., 2008).
• Hardy, G. H.; Littlewood, J. E. (1921), «The zeros of Riemann's zeta-function on the critical line», Math. Z. 10 (3–4): 283-317, S2CID 126338046, doi:10.1007/BF01211614 .
• Haselgrove, C. B. (1958), «A disproof of a conjecture of Pólya», Mathematika 5 (2): 141-145, ISSN 0025-5793, MR 0104638, Zbl 0085.27102, doi:10.1112/S0025579300001480 . Reprinted in (Borwein et al., 2008).
• Haselgrove, C. B.; Miller, J. C. P. (1960), Tables of the Riemann zeta function, Royal Society Mathematical Tables, Vol. 6, Cambridge University Press, ISBN 978-0-521-06152-0, MR 0117905 . Review
• Hutchinson, J. I. (1925), «On the Roots of the Riemann Zeta-Function», Transactions of the American Mathematical Society 27 (1): 49-60, JSTOR 1989163, doi:10.2307/1989163 .
• Ingham, A.E. (1932), The Distribution of Prime Numbers, Cambridge Tracts in Mathematics and Mathematical Physics 30, Cambridge University Press .. Reprinted 1990, ISBN 978-0-521-39789-6, MR 1074573
• Ireland, Kenneth; Rosen, Michael (1990), A Classical Introduction to Modern Number Theory (Second edition), New York: Springer, ISBN 0-387-97329-X .
• Ivić, A. (1985), The Riemann Zeta Function, New York: John Wiley & Sons, ISBN 978-0-471-80634-9, MR 0792089 . (Reprinted by Dover 2003)
• Ivić, Aleksandar (2008), «On some reasons for doubting the Riemann hypothesis», en Borwein, Peter; Choi, Stephen; Rooney, Brendan et al., eds., The Riemann Hypothesis: A Resource for the Afficionado and Virtuoso Alike, CMS Books in Mathematics, New York: Springer, pp. 131-160, ISBN 978-0-387-72125-5, arXiv:math.NT/0311162  Se sugiere usar |número-editores= (ayuda).
• Karatsuba, A. A. (1984a), «Zeros of the function ζ(s) on short intervals of the critical line», Izv. Akad. Nauk SSSR, Ser. Mat. (en ruso) 48 (3): 569-584, MR 0747251 .
• Karatsuba, A. A. (1984b), «Distribution of zeros of the function ζ(1/2 + it)», Izv. Akad. Nauk SSSR, Ser. Mat. (en ruso) 48 (6): 1214-1224, MR 0772113 .
• Karatsuba, A. A. (1985), «Zeros of the Riemann zeta-function on the critical line», Trudy Mat. Inst. Steklov. (en ruso) (167): 167-178, MR 0804073 .
• Karatsuba, A. A. (1992), «On the number of zeros of the Riemann zeta-function lying in almost all short intervals of the critical line», Izv. Ross. Akad. Nauk, Ser. Mat. (en ruso) 56 (2): 372-397, Bibcode:1993IzMat..40..353K, MR 1180378, doi:10.1070/IM1993v040n02ABEH002168 .
• Karatsuba, A. A.; Voronin, S. M. (1992), The Riemann zeta-function, de Gruyter Expositions in Mathematics 5, Berlin: Walter de Gruyter & Co., ISBN 978-3-11-013170-3, MR 1183467, doi:10.1515/9783110886146 .
• Keating, Jonathan P.; Snaith, N. C. (2000), «Random matrix theory and ζ(1/2 + it)», Communications in Mathematical Physics 214 (1): 57-89, Bibcode:2000CMaPh.214...57K, MR 1794265, S2CID 11095649, doi:10.1007/s002200000261 .
• Knapowski, S. (1962), «On sign-changes of the difference ${\displaystyle \pi (x)-\operatorname {li} x}$», Acta Arithmetica 7: 107-119, MR 133308, doi:10.4064/aa-7-2-107-119 .
• Knauf, Andreas (1999), «Number theory, dynamical systems and statistical mechanics», Reviews in Mathematical Physics 11 (8): 1027-1060, Bibcode:1999RvMaP..11.1027K, MR 1714352, doi:10.1142/S0129055X99000325 .
• von Koch, Niels Helge (1901), «Sur la distribution des nombres premiers», Acta Mathematica 24: 159-182, S2CID 119914826, doi:10.1007/BF02403071 .
• Kurokawa, Nobushige (1992), «Multiple zeta functions: an example», Zeta functions in geometry (Tokyo, 1990), Adv. Stud. Pure Math. 21, Tokyo: Kinokuniya, pp. 219-226, MR 1210791 .
• Lapidus, Michel L. (2008), In search of the Riemann zeros, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-4222-5, MR 2375028, doi:10.1090/mbk/051 .
• Plantilla:Eom
• Lehmer, D. H. (1956), «Extended computation of the Riemann zeta-function», Mathematika 3 (2): 102-108, MR 0086083, doi:10.1112/S0025579300001753 .
• Leichtnam, Eric (2005), «An invitation to Deninger's work on arithmetic zeta functions», Geometry, spectral theory, groups, and dynamics, Contemp. Math. 387, Providence, RI: Amer. Math. Soc., pp. 201-236, MR 2180209, doi:10.1090/conm/387/07243 ..
• Levinson, N. (1974), «More than one-third of the zeros of Riemann's zeta function are on σ = 1/2», Advances in Mathematics 13 (4): 383-436, MR 0564081, doi:10.1016/0001-8708(74)90074-7 .
• Littlewood, J. E. (1962), «The Riemann hypothesis», The scientist speculates: an anthology of partly baked idea, New York: Basic books .
• van de Lune, J.; te Riele, H. J. J.; Winter, D. T. (1986), «On the zeros of the Riemann zeta function in the critical strip. IV», Mathematics of Computation 46 (174): 667-681, JSTOR 2008005, MR 829637, doi:10.2307/2008005 .
• Massias, J.-P.; Nicolas, Jean-Louis; Robin, G. (1988), «Évaluation asymptotique de l'ordre maximum d'un élément du groupe symétrique», Acta Arithmetica 50 (3): 221-242, MR 960551, doi:10.4064/aa-50-3-221-242 .
• Mazur, Barry; Stein, William (2015), Prime Numbers and the Riemann Hypothesis .
• Montgomery, Hugh L. (1973), «The pair correlation of zeros of the zeta function», Analytic number theory, Proc. Sympos. Pure Math. XXIV, Providence, R.I.: American Mathematical Society, pp. 181-193, MR 0337821 . Reprinted in (Borwein et al., 2008).
• Montgomery, Hugh L. (1983), «Zeros of approximations to the zeta function», en Erdős, Paul, ed., Studies in pure mathematics. To the memory of Paul Turán, Basel, Boston, Berlin: Birkhäuser, pp. 497-506, ISBN 978-3-7643-1288-6, MR 820245 .
• Montgomery, Hugh L.; Vaughan, Robert C. (2007), Multiplicative Number Theory I. Classical Theory, Cambridge studies in advanced mathematics 97, Cambridge University Press ..ISBN 978-0-521-84903-6
• Nicely, Thomas R. (1999), «New maximal prime gaps and first occurrences», Mathematics of Computation 68 (227): 1311-1315, Bibcode:1999MaCom..68.1311N, MR 1627813, doi:10.1090/S0025-5718-99-01065-0 ..
• Nyman, Bertil (1950), On the One-Dimensional Translation Group and Semi-Group in Certain Function Spaces, PhD Thesis, University of Uppsala: University of Uppsala, MR 0036444 .
• Odlyzko, A. M.; te Riele, H. J. J. (1985), «Disproof of the Mertens conjecture», Journal für die reine und angewandte Mathematik 1985 (357): 138-160, MR 783538, S2CID 13016831, doi:10.1515/crll.1985.357.138, archivado desde el original el 11 de julio de 2012 .
• Odlyzko, A. M. (1987), «On the distribution of spacings between zeros of the zeta function», Mathematics of Computation 48 (177): 273-308, JSTOR 2007890, MR 866115, doi:10.2307/2007890 .
• Odlyzko, A. M. (1990), «Bounds for discriminants and related estimates for class numbers, regulators and zeros of zeta functions: a survey of recent results», Séminaire de Théorie des Nombres de Bordeaux, Série 2 2 (1): 119-141, MR 1061762, doi:10.5802/jtnb.22 .
• Odlyzko, A. M. (1992), The 10²⁰-th zero of the Riemann zeta function and 175 million of its neighbors . This unpublished book describes the implementation of the algorithm and discusses the results in detail.
• Odlyzko, A. M. (1998), The 10²¹st zero of the Riemann zeta function .
• Ono, Ken; Soundararajan, K. (1997), «Ramanujan's ternary quadratic form», Inventiones Mathematicae 130 (3): 415-454, Bibcode:1997InMat.130..415O, S2CID 122314044, doi:10.1007/s002220050191 .
• Patterson, S. J. (1988), An introduction to the theory of the Riemann zeta-function, Cambridge Studies in Advanced Mathematics 14, Cambridge University Press, ISBN 978-0-521-33535-5, MR 933558, doi:10.1017/CBO9780511623707 .
• Platt, Dave; Trudgian, Tim (January 2021), «The Riemann hypothesis is true up to ${\displaystyle 3\cdot 10^{12}}$», Bulletin of the London Mathematical Society (Wiley) 53 (3): 792-797, S2CID 234355998, arXiv:2004.09765, doi:10.1112/blms.12460 .
• Radziejewski, Maciej (2007), «Independence of Hecke zeta functions of finite order over normal fields», Transactions of the American Mathematical Society 359 (5): 2383-2394, MR 2276625, doi:10.1090/S0002-9947-06-04078-5, «There are infinitely many nonisomorphic algebraic number fields whose Dedekind zeta functions have infinitely many nontrivial multiple zeros.» .
• Ribenboim, Paulo (1996), The New Book of Prime Number Records, New York: Springer, ISBN 0-387-94457-5 .
• Riemann, Bernhard (1859), «Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse», Monatsberichte der Berliner Akademie .. In Gesammelte Werke, Teubner, Leipzig (1892), Reprinted by Dover, New York (1953). Original manuscript (with English translation). Reprinted in (Borwein et al., 2008) and (Edwards, 1974)
• Riesel, Hans; Göhl, Gunnar (1970), «Some calculations related to Riemann's prime number formula», Mathematics of Computation 24 (112): 969-983, JSTOR 2004630, MR 0277489, doi:10.2307/2004630 .
• Riesz, M. (1916), «Sur l'hypothèse de Riemann», Acta Mathematica 40: 185-190, doi:10.1007/BF02418544 .
• Robin, G. (1984), «Grandes valeurs de la fonction somme des diviseurs et hypothèse de Riemann», Journal de Mathématiques Pures et Appliquées, Neuvième Série 63 (2): 187-213, MR 774171 .
• Rodgers, Brad; Tao, Terence (2020), «The de Bruijn–Newman constant is non-negative», Forum of Mathematics 8: e6, 62, MR 4089393, arXiv:1801.05914, doi:10.1017/fmp.2020.6 .; see also announcement on Tao's blog, January 19, 2018
• Rosser, J. Barkley; Yohe, J. M.; Schoenfeld, Lowell (1969), «Rigorous computation and the zeros of the Riemann zeta-function. (With discussion)», Information Processing 68 (Proc. IFIP Congress, Edinburgh, 1968), Vol. 1: Mathematics, Software, Amsterdam: North-Holland, pp. 70-76, MR 0258245 .
• Rudin, Walter (1973), Functional Analysis, 1st edition (January 1973), New York: McGraw-Hill, ISBN 0-070-54225-2 .
• Salem, Raphaël (1953), «Sur une proposition équivalente à l'hypothèse de Riemann», Les Comptes rendus de l'Académie des sciences 236: 1127-1128, MR 0053148 .
• Sarnak, Peter (2005), Problems of the Millennium: The Riemann Hypothesis (2004), Clay Mathematics Institute, consultado el 28 de julio de 2015 . Reprinted in (Borwein et al., 2008).
• Schoenfeld, Lowell (1976), «Sharper bounds for the Chebyshev functions θ(x) and ψ(x). II», Mathematics of Computation 30 (134): 337-360, JSTOR 2005976, MR 0457374, doi:10.2307/2005976 .
• Schumayer, Daniel; Hutchinson, David A. W. (2011), «Physics of the Riemann Hypothesis», Reviews of Modern Physics 83 (2): 307-330, Bibcode:2011RvMP...83..307S, S2CID 119290777, arXiv:1101.3116, doi:10.1103/RevModPhys.83.307 .
• Selberg, Atle (1942), «On the zeros of Riemann's zeta-function», SKR. Norske Vid. Akad. Oslo I. 10: 59 pp, MR 0010712 .
• Selberg, Atle (1946), «Contributions to the theory of the Riemann zeta-function», Arch. Math. Naturvid. 48 (5): 89-155, MR 0020594 .
• Selberg, Atle (1956), «Harmonic analysis and discontinuous groups in weakly symmetric Riemannian spaces with applications to Dirichlet series», J. Indian Math. Soc., New Series 20: 47-87, MR 0088511 .
• Serre, Jean-Pierre (1969–1970), «Facteurs locaux des fonctions zeta des varietés algébriques (définitions et conjectures)», Séminaire Delange-Pisot-Poitou 19 .
• Sheats, Jeffrey T. (1998), «The Riemann hypothesis for the Goss zeta function for F_q[T]», Journal of Number Theory 71 (1): 121-157, MR 1630979, S2CID 119703557, arXiv:math/9801158, doi:10.1006/jnth.1998.2232 .
• Siegel, C. L. (1932), «Über Riemanns Nachlaß zur analytischen Zahlentheorie», Quellen Studien zur Geschichte der Math. Astron. Und Phys. Abt. B: Studien 2: 45-80 . Reprinted in Gesammelte Abhandlungen, Vol. 1. Berlin: Springer-Verlag, 1966.
• Speiser, Andreas (1934), «Geometrisches zur Riemannschen Zetafunktion», Mathematische Annalen 110: 514-521, JFM 60.0272.04, S2CID 119413347, doi:10.1007/BF01448042, archivado desde el original el 27 de junio de 2015 .
• Spira, Robert (1968), «Zeros of sections of the zeta function. II», Mathematics of Computation 22 (101): 163-173, JSTOR 2004774, MR 0228456, doi:10.2307/2004774 .
• Stein, William; Mazur, Barry (2007), What is Riemann's Hypothesis?, archivado desde el original el 27 de marzo de 2009 .
• Suzuki, Masatoshi (2011), «Positivity of certain functions associated with analysis on elliptic surfaces», Journal of Number Theory 131 (10): 1770-1796, doi:10.1016/j.jnt.2011.03.007 .
• Titchmarsh, Edward Charles (1935), «The Zeros of the Riemann Zeta-Function», Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences (The Royal Society) 151 (873): 234-255, Bibcode:1935RSPSA.151..234T, JSTOR 96545, S2CID 263711590, doi:10.1098/rspa.1935.0146 .
• Titchmarsh, Edward Charles (1936), «The Zeros of the Riemann Zeta-Function», Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences (The Royal Society) 157 (891): 261-263, Bibcode:1936RSPSA.157..261T, JSTOR 96692, arXiv:1004.4143, doi:10.1098/rspa.1936.0192 .
• Titchmarsh, Edward Charles (1986), The theory of the Riemann zeta-function (2nd edición), The Clarendon Press Oxford University Press, ISBN 978-0-19-853369-6, MR 882550 .
• Trudgian, Timothy S. (2014), «An improved upper bound for the argument of the Riemann zeta function on the critical line II», J. Number Theory 134: 280-292, arXiv:1208.5846, doi:10.1016/j.jnt.2013.07.017 .
• Trudgian, Timothy (2011), «On the success and failure of Gram's Law and the Rosser Rule», Acta Arithmetica 125 (3): 225-256, doi:10.4064/aa148-3-2 .
• Turán, Paul (1948), «On some approximative Dirichlet-polynomials in the theory of the zeta-function of Riemann», Danske Vid. Selsk. Mat.-Fys. Medd. 24 (17): 36, MR 0027305 . Reprinted in (Borwein et al., 2008).
• Turing, Alan M. (1953), «Some calculations of the Riemann zeta-function», Proceedings of the London Mathematical Society, Third Series 3: 99-117, MR 0055785, doi:10.1112/plms/s3-3.1.99 .
• de la Vallée-Poussin, Ch.J. (1896), «Recherches analytiques sur la théorie des nombres premiers», Ann. Soc. Sci. Bruxelles 20: 183-256 .
• de la Vallée-Poussin, Ch.J. (1899–1900), «Sur la fonction ζ(s) de Riemann et la nombre des nombres premiers inférieurs à une limite donnée», Mem. Couronnes Acad. Sci. Belg. 59 (1) . Reprinted in (Borwein et al., 2008).
• Weil, André (1948), Sur les courbes algébriques et les variétés qui s'en déduisent, Actualités Sci. Ind., no. 1041 = Publ. Inst. Math. Univ. Strasbourg 7 (1945), Hermann et Cie., Paris, MR 0027151 .
• Weil, André (1949), «Numbers of solutions of equations in finite fields», Bulletin of the American Mathematical Society 55 (5): 497-508, MR 0029393, doi:10.1090/S0002-9904-1949-09219-4 . Reprinted in Oeuvres Scientifiques/Collected Papers by Andre Weil ISBN 0-387-90330-5
• Weinberger, Peter J. (1973), «On Euclidean rings of algebraic integers», Analytic number theory ( St. Louis Univ., 1972), Proc. Sympos. Pure Math. 24, Providence, R.I.: Amer. Math. Soc., pp. 321-332, MR 0337902 .
• Wiles, Andrew (2000), «Twenty years of number theory», Mathematics: frontiers and perspectives, Providence, R.I.: American Mathematical Society, pp. 329-342, ISBN 978-0-8218-2697-3, MR 1754786 .
• Zagier, Don (1977), «The first 50 million prime numbers», Math. Intelligencer (Springer) 1: 7-19, MR 643810, S2CID 189886510, doi:10.1007/BF03039306, archivado desde el original el 27 de marzo de 2009 .
• Zagier, Don (1981), «Eisenstein series and the Riemann zeta function», Automorphic forms, representation theory and arithmetic (Bombay, 1979), Tata Inst. Fund. Res. Studies in Math. 10, Tata Inst. Fundamental Res., Bombay, pp. 275-301, MR 633666 .

Exposiciones populares

• Sabbagh, Karl (2003a), The greatest unsolved problem in mathematics, Farrar, Straus and Giroux, New York, ISBN 978-0-374-25007-2, MR 1979664 .
• Sabbagh, Karl (2003b), Dr. Riemann's zeros, Atlantic Books, London, ISBN 978-1-843-54101-1 .
• du Sautoy, Marcus (2003), The music of the primes, HarperCollins Publishers, ISBN 978-0-06-621070-4, MR 2060134 .
• Rockmore, Dan (2005), Stalking the Riemann hypothesis, Pantheon Books, ISBN 978-0-375-42136-5, MR 2269393 .
• Derbyshire, John (2003), Prime Obsession, Joseph Henry Press, Washington, DC, ISBN 978-0-309-08549-6, MR 1968857 .
• Watkins, Matthew (2015), Mystery of the Prime Numbers, Liberalis Books, ISBN 978-1782797814, MR 0000000 .
• Frenkel, Edward (2014), The Riemann Hypothesis Numberphile, Mar 11, 2014 (video)
• Nahin, Paul J. (2021). In Pursuit of Zeta-3: The World's Most Mysterious Unsolved Math Problem. Princeton University Press. ISBN 978-0691206073. 

Note: Derbyshire 2003, Rockmore 2005, Sabbagh 2003a, Sabbagh 2003b, Sautoy 2003, and Watkins 2015 are non-technical. Edwards 1974, Patterson 1988, Borwein/Choi/Rooney/Weirathmueller 2008, Mazur/Stein 2015, Broughan 2017, and Nahin 2021 give mathematical introductions. Titchmarsh 1986, Ivić 1985, and Karatsuba/Voronin 1992 are advanced monographs.

Enlaces externos

• (en) The Riemann Hypothesis in a Nutshell Archivado el 15 de junio de 2008 en Wayback Machine.
• (en) Andrew Odlyzko: Tables of zeros of the Riemann zeta function
• (en) Riemann zeros Quantum chaos
• (en) Zetagrid
• (en) Algoritmos para calcular los ceros de la función de Riemann, por Michael Rubinstein
• (en) Consecuencias de la Hipótesis de Riemann
• Wikimedia Commons alberga una categoría multimedia sobre Hipótesis de Riemann.
• American Institute of Mathematics, Riemann hypothesis
• Zeroes database, 103 800 788 359 zeroes
• Apostol, Tom, Where are the zeros of zeta of s? . Poem about the Riemann hypothesis, sung by John Derbyshire.
• Borwein, Peter, The Riemann Hypothesis, archivado desde el original el 27 de marzo de 2009 . (Slides for a lecture)
• Conrad, K. (2010), Consequences of the Riemann hypothesis .
• Conrey, J. Brian; Farmer, David W, Equivalences to the Riemann hypothesis, archivado desde el original el 16 de marzo de 2010 .
• Gourdon, Xavier; Sebah, Pascal (2004), Computation of zeros of the Zeta function . (Reviews the GUE hypothesis, provides an extensive bibliography as well).
• Odlyzko, Andrew, Home page . including papers on the zeros of the zeta function and tables of the zeros of the zeta function
• Odlyzko, Andrew (2002), Zeros of the Riemann zeta function: Conjectures and computations . Slides of a talk
• Pegg, Ed (2004), Ten Trillion Zeta Zeros, Math Games website, archivado desde el original el 2 de noviembre de 2004, consultado el 20 de octubre de 2004 .. A discussion of Xavier Gourdon's calculation of the first ten trillion non-trivial zeros
• Rubinstein, Michael, algorithm for generating the zeros, archivado desde el original el 27 de abril de 2007 ..
• du Sautoy, Marcus (2006), Prime Numbers Get Hitched, Seed Magazine, archivado desde el original el 22 de septiembre de 2017, consultado el 27 de marzo de 2006 .
• Watkins, Matthew R. (27 de febrero de 2021), Proposed (dis)proofs of the Riemann Hypothesis, archivado desde el original el December 9, 2022 .
• Zetagrid (2002) A distributed computing project that attempted to disprove Riemann's hypothesis; closed in November 2005