Polynomdivision
Die Polynomdivision, auch Partialdivision genannt, ist ein mathematisches Rechenverfahren, bei dem ein Polynom durch ein anderes dividiert wird. Das Ergebnis ist ein „Ganzteil“-Polynom und evtl. ein Restpolynom. Das Verfahren verläuft analog zur üblichen und in der Schule gelehrten Division von Zahlen mit Rest. Während dort vorübergehend kleinere Dezimalstellen ignoriert werden und die nächste Ziffer des Ergebnisses ggf. erraten wird, ist hier der nächste Koeffizient durch Division der verbliebenen höchsten Koeffizienten exakt bestimmt.
Allgemein
Informell
Im Folgenden seien und natürliche Zahlen einschließlich Null () und der Einfachheit halber die Größen und stets ganze Zahlen, also Elemente von . Hat man nun zwei Polynome, etwa
und
so kann man sie unter gewissen formalen Voraussetzungen ähnlich wie ganze Zahlen durcheinander dividieren, also die Rechenaufgabe
lösen. Im Ergebnis finden sich dann zwei Polynome: Ein Polynom , das dem Ganzzahlquotienten in der Zahlendivision mit Rest entspricht, und ein Polynom , das sich nicht mehr weiter durch teilen lässt und das dem Rest in der Zahlendivision entspricht:
oder in Analogie zur Schulschreibweise
Das Verfahren zum Auffinden dieser Lösung, bestehend aus und , ist die Polynomdivision.
Dass sich hiernach nicht weiter durch teilen lässt, ist gleichbedeutend damit, dass der Polynomgrad von kleiner ist als der von , weshalb dies in der formalen Definition der Rechenvorschrift (Algorithmus) auch als Abbruchbedingung gefordert wird. In der Zahlendivision mit Rest wird stattdessen gefordert, dass der Rest kleiner als der Divisor ist. Beide Nebenbedingungen sorgen im jeweiligen Verfahren dafür, dass der Rest eindeutig bestimmt ist.
Bei der formalen Definition des Verfahrens werden einige zusätzliche Bedingungen beachtet. Das kommt daher, dass man Polynome im Allgemeinen viel weitläufiger definieren kann, als es hier zur einfacheren Erklärung geschehen ist oder man es zum Beispiel aus der Schule kennt. Die Koeffizienten eines Polynoms etwa können dann aus beliebigen Ringen stammen. Dann dürfen aber wiederum die Koeffizienten der beiden Polynome nicht aus verschiedenen Ringen stammen. Daher definiert man, dass die Polynome in einem gemeinsamen Polynomring liegen müssen. Auch reicht es nicht mehr zu fordern, dass der „höchste“ Koeffizient (Leitkoeffizient) von nur ungleich Null sein müsse. Vielmehr muss man fordern, dass er zudem eine Einheit des Ringes sein muss. Oder es wird das unten beschriebene Verfahren der Pseudo-Division angewendet.
Formal
Bei der Polynomdivision sind zwei Polynome und eines Polynomringes gegeben, wobei ein kommutativer Ring mit und der Leitkoeffizient von eine Einheit in ist, und es wird die Gleichung
nach den gesuchten Polynomen und gelöst, und zwar so, dass der Grad von kleiner als der von ist.
Anmerkungen
- Wegen sind die Polynome und in eindeutig bestimmt.
- Die Polynomdivision ist im Allgemeinen keine innere Verknüpfung auf , da sich als Ergebnis der Division zweier Polynome im Allgemeinen nicht ein einzelnes, sondern zwei Polynome in ergeben und sich somit keine Zuordnung der Form machen lässt. Ist das jedoch im Einzelfall möglich, so wird zu einem Körper mit der Polynomdivision als Umkehrung der Polynommultiplikation.
- Ist die Polynomdivision für jedes beliebige Paar von zwei Polynomen aus möglich, so wird zu einem euklidischen Ring bzgl. der Polynomgrad-Funktion. Das ist genau dann der Fall, wenn ein Körper ist.
Anwendungen
- Eine Anwendung ist das Lösen von Gleichungen höheren Grades. Wenn eine Lösung (Nullstelle) bekannt ist, findet die Polynomdivision Anwendung, um den Grad der Gleichung um Eins zu senken. Diese Vorgehensweise wird „Abspalten einer Nullstelle“ genannt.
- Eine weitere Anwendung findet die Polynomdivision bei der Kurvendiskussion mit der Bestimmung der Näherungskurven einer rationalen Funktion.
- Bei der Partialbruchzerlegung rationaler Funktionen wird die Polynomdivision ebenfalls benötigt.
- Bei der Berechnung von Prüfsummen findet die Polynomdivision über dem Ring der ganzen Zahlen modulo 2 Anwendung, siehe CRC-Polynom.
- Nach erfolgter Polynomdivision kann man dasselbe Verfahren auf Divisor und Rest erneut anwenden und so einen weiteren Rest berechnen, und so weiter. Man erhält dann eine sogenannte Polynomrestfolge.
Berechnung
Manueller Ablauf
Das Verfahren funktioniert für Polynome mit ganzzahligen Koeffizienten genau so wie die schriftliche Division ganzer Zahlen mit Rest und kann mit dem gleichen Schema (Verfahren, Vorgehensweise) gelöst werden. Hier werden die einzelnen Schritte am Beispiel
erläutert:
- Wie bei der Division ganzer Zahlen wird zuerst der Summand höchsten Grades des Polynoms eliminiert. Dazu wird zunächst der Summand höchsten Grades von durch den Summanden höchsten Grades von dividiert. Das Ergebnis ist . Danach wird mit multipliziert und von subtrahiert.
- Es bleibt der Rest . Sein Grad ist nicht kleiner als der des Divisors.
- Im nächsten Schritt wird von diesem Rest der Summand höchsten Grades eliminiert, bis in mehreren solchen Schritten ein Rest entsteht (hier: ), der nicht mehr eliminiert werden kann, weil sein Grad kleiner als der Grad des Divisors ist.
- Weitere Beispiele
Algorithmus
Das folgende Code-Fragment in BASIC zeigt den Kern der Berechnung:
For i = GradZ - GradN To 0 Step -1 Quotient(i) = Zähler(i + GradN) / Nenner(GradN) For j = GradN To 0 Step -1 Zähler(i + j) = Zähler(i + j) - Nenner(j) * Quotient(i) Next j Next i For j = GradN - 1 To 0 Step -1 Rest(j) = Zähler(j) Next j
Die Variable Zähler() ist ein Feld (Array), welches die Koeffizienten des Zählerpolynoms enthält, so dass Zähler(i) den Koeffizienten der Potenz enthält. Entsprechend ist Nenner() ein weiteres Feld, welches in gleicher Art die Koeffizienten des Nennerpolynoms enthält. Das Ergebnis sind zwei Polynome, welche in Quotient() und Rest() ausgegeben werden. Die Variablen GradN und GradZ enthalten den jeweiligen Polynomgrad von Zähler und Nenner.
In einem optimierten Programm könnte man die innere Schleife von 0 bis GradN-1 laufen lassen und die Ergebnisse in Zähler() zurückschreiben, so dass die Variablen Quotient() und Rest() entfallen würden. Der Einfachheit halber wurde hier darauf verzichtet.
Pseudo-Division
Die oben beschriebene Methode zur Polynomdivision ist nur dann anwendbar, wenn der Leitkoeffizient des Divisors eine Einheit im Grundring ist. Das ist immer der Fall, wenn der Grundring ein Körper ist. Über allgemeinen Grundringen muss das jedoch nicht immer der Fall sein. Deswegen wird eine sogenannte Pseudo-Division definiert, die über allen Integritätsringen funktioniert. Gelöst wird dabei nicht die obige Gleichung, sondern die leicht variierte Gleichung
wobei die Polynome und vorgegeben sind und eine Konstante sowie Polynome und gesucht werden. Auch hier soll wieder der Grad von kleiner als derjenige von sein.
Das Vorgehen ist ähnlich der normalen Polynomdivision. Allerdings werden im Divisionsschritt nicht nur das Polynom , sondern auch mit geeigneten Faktoren multipliziert, um zu erreichen, dass sich die Leitkoeffizienten gegenseitig herauslöschen.
Beispiel
Als Beispiel soll eine Pseudo-Division im Polynomring über den ganzen Zahlen durchgeführt werden. Seien
Eine normale Polynomdivision ist hier nicht möglich, da , der Leitkoeffizienten von , in nicht invertierbar ist. Wir können aber mit multiplizieren. Nun kann man mit multipliziert abziehen und erhält
Der Grad von ist dabei kleiner als derjenige von aber noch nicht kleiner als der von . Ziehen wir nun von diesem Zwischenergebnis -mal ab, erhalten wir
Da als konstantes Polynom einen kleineren Grad als besitzt, sind wir hier fertig. Rückwärts einsetzen ergibt
oder umgeformt
Eine Probe bestätigt dies.
Algorithmus
Das Vorgehen soll nun noch durch den Algorithmus illustriert werden. Dieser rekursive Algorithmus hat als Argumente zwei Polynome und , wobei nicht das Nullpolynom sein darf, sowie die Variable , bezüglich der die Pseudodivision zu erfolgen hat. Das Ergebnis ist ein Tripel bestehend aus Polynomen und sowie einer Konstanten , so dass und gilt.
pseudoDivision(p, q, x) =
if d < 0
then (1, 0, p)
else (c * a, c * t + s, r) where
d = grad(p, x) - grad(q, x)
a = lcoeff(q, x)
b = lcoeff(p, x)
t = b*xd
(c,q,r) = pseudoDivision(a*p - t*q, q, x)
Hierbei liefert den Grad sowie den Leitkoeffizienten eines Polynomes. Man kann noch weitere Verbesserungen am Algorithmus vornehmen, indem man etwa wie im Beispiel die Multiplikation mit x unterlässt, wenn sie nicht notwendig ist.
Division durch Linearfaktor
Will man bei einer Gleichung
den Linearfaktor einer Lösung abspalten, so ergibt sich das um ein Grad reduzierte Polynom
mit den Koeffizienten
- Beispiel:
Die Polynomgleichung
hat die Lösung
Das Restpolynom hat also die Koeffizienten
und lautet:
Horner-Schema
Mit Leitkoeffizient 1 kann schneller mit dem Horner-Schema (zur Funktionswert-Berechnung eines Polynoms) gearbeitet werden. Interessant ist die Umkehrung: man kann mit der Polynomdivision auch Funktionswerte bestimmen. Beispiel: mit
Polynomdivision liefert:
Nach Multiplikation mit sieht man, dass der Rest 22 der Funktionswert ist.
Verallgemeinerung auf Polynomringe in mehreren Unbestimmten
Es existiert eine verallgemeinerte Polynomdivision in multivariablen Polynomringen , wenn ein Körper ist. Dabei werden einige Abstriche in Kauf genommen, wie beispielsweise die Eindeutigkeit.
Literatur
- Peter Hartmann: Mathematik für Informatiker. Vieweg+Teubner, 2006, ISBN 3-8348-0096-1, S. 88–90 (Auszug in der Google-Buchsuche)
- Schülerduden Mathematik II. Dudenverlag, 2004, ISBN 3-411-04275-3, S. 327–328
- Charles D. Miller, Margaret L. Lial, David I. Schneider: Fundamentals of College Algebra. 3. überarbeitete Auflage. Scott & Foresman / Little & Brown Higher Education, 1990, ISBN 0-673-38638-4, S. 24–26
Weblinks
- JavaScript berechnet Polynomdivision und erzeugt Übungsaufgaben
- Polynomdivision Rechner mit Rechenweg
















![{\displaystyle R[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ce54622cb380383ab3a42441b056626ea0d2440)




![{\displaystyle R[x]\times R[x]\rightarrow R[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8eaa91131672964ec0929f93b15d869aac0170a)











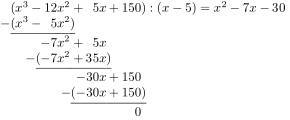
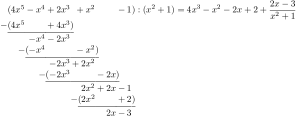



![{\displaystyle \mathbb {Z} [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d4da3ac703cc7721ebba91a53f6752de7157124)









































![{\displaystyle K[x_{1},x_{2},\ldots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd5197b9611cbdba8f0e65fec4069515eb9142fc)










