Gauß-Newton-Verfahren

Das Gauß-Newton-Verfahren (nach Carl Friedrich Gauß und Isaac Newton) ist ein numerisches Verfahren zur Lösung nichtlinearer Minimierungsprobleme nach der Methode der kleinsten Quadrate. Das Verfahren ist verwandt mit dem Newton-Verfahren zur Lösung nichtlinearer Optimierungsprobleme, hat jedoch den Vorteil, dass die für das Newton-Verfahren notwendige Berechnung der 2. Ableitung entfällt. Speziell für große Probleme mit mehreren zehntausend Parametern ist die Berechnung der 2. Ableitung oft ein limitierender Faktor.

Das Optimierungsproblem

Das Gauß-Newton-Verfahren löst Probleme bei denen das Minimum einer Summe von Quadraten stetig differenzierbarer Funktionen ${\displaystyle f_{i}\colon \mathbb {R} ^{n}\to \mathbb {R} }$ gesucht ist, also

${\displaystyle \min _{x\in \mathbb {R} ^{n}}\left\{{\frac {1}{2}}\sum _{i=1}^{m}\left(f_{i}(x)\right)^{2}\right\}}$

mit ${\displaystyle m\geq n}$. Mit der euklidischen Norm ${\displaystyle \|\cdot \|}$ lässt sich das auch schreiben als

${\displaystyle \min _{x\in \mathbb {R} ^{n}}\left\{{\frac {1}{2}}\|f(x)\|^{2}\right\}}$

mit ${\displaystyle f=(f_{1},\dotsc ,f_{m})\colon \mathbb {R} ^{n}\to \mathbb {R} ^{m}}$. Probleme dieser Form kommen in der Praxis häufig vor, insbesondere ist das nichtlineare Problem ${\displaystyle f(x)=0}$ äquivalent zur Minimierung von ${\displaystyle {\tfrac {1}{2}}\|f(x)\|^{2}}$ unter der Voraussetzung, dass ${\displaystyle f}$ eine Nullstelle besitzt.

Das Gauß-Newton-Verfahren wird sehr häufig verwendet, um nichtlineare Ausgleichsprobleme zu lösen. In diesem Fall ergeben sich die Komponentenfunktionen ${\displaystyle f_{i}(x)}$ als Abweichung einer Modellfunktion ${\displaystyle g(x)}$ von bekannten Beobachtungen bzw. Messwerten ${\displaystyle y_{i}}$, also ${\displaystyle f_{i}(x)=g(x)-y_{i}}$. Ist die Modellfunktion ${\displaystyle g}$ eine lineare Abbildung, ergibt sich der Standardfall der Methode der kleinsten Quadrate mit linearer Modellfunktion.

Die Methode

Die Grundidee des Gauß-Newton-Verfahrens besteht darin, die Zielfunktion ${\displaystyle f}$ zu linearisieren und die Linearisierung im Sinne der kleinsten Quadrate zu optimieren. Die Linearisierung, also die Taylorentwicklung 1. Ordnung, von ${\displaystyle f}$ im Punkt ${\displaystyle x^{0}\in \mathbb {R} ^{n}}$ lautet

${\displaystyle {\tilde {f}}(x)=f(x^{0})+\nabla f(x^{0})^{T}(x-x^{0})}$.

Die Matrix ${\displaystyle \nabla f(x^{0})^{T}}$ ist die Jacobi-Matrix und wird oft mit ${\displaystyle J}$ bezeichnet. Man erhält das lineare kleinste-Quadrate Problem

${\displaystyle \min _{x\in \mathbb {R} ^{n}}\left\{{\frac {1}{2}}\|{\tilde {f}}(x)\|^{2}={\frac {1}{2}}\|J(x-x^{0})+f(x^{0})\|^{2}\right\}}$,

mit Gradient ${\displaystyle \nabla {\frac {1}{2}}\left\Vert {\tilde {f}}(x)\right\Vert ^{2}=J^{T}\left(J(x-x^{0})+f(x^{0})\right)}$.

Nullsetzen des Gradienten liefert die sogenannten Normalgleichungen

${\displaystyle J^{T}J(x-x^{0})=-J^{T}f(x^{0})}$

mit der expliziten Lösung

${\displaystyle x=x^{0}-\left(J^{T}J\right)^{-1}J^{T}f(x^{0})}$.

Daraus ergibt sich direkt der Gauß-Newton-Iterationsschritt

${\displaystyle x^{k+1}=x^{k}-\alpha ^{k}\left((J|_{x^{k}})^{T}J|_{x^{k}}\right)^{-1}(J|_{x^{k}})^{T}f(x^{k})}$,

wobei ${\displaystyle J|_{x^{k}}}$ deutlich macht, dass die Jacobi-Matrix an der Stelle ${\displaystyle x^{k}}$ ausgewertet wird und ${\displaystyle \alpha ^{k}\geq 0}$ eine Schrittweite ist.

Um das lineare Gleichungssystem im Gauß-Newton-Iterationsschritt zu lösen gibt es verschiedene Möglichkeiten abhängig von der Problemgröße und der Struktur:^[1]

• Kleine Probleme (${\displaystyle n<1000,\ m<10000}$) werden am besten mit der QR-Zerlegung gelöst
• Für große Probleme bietet sich die Cholesky-Zerlegung an, da die Matrix ${\displaystyle J^{T}J}$ per Konstruktion symmetrisch ist. Für dünnbesetzte ${\displaystyle J^{T}J}$ gibt es speziell angepasste Cholesky-Varianten
• Als allgemeine Möglichkeit kann das CG-Verfahren verwendet werden, wobei hier üblicherweise eine Vorkonditionierung notwendig ist

Konvergenz

Der Update-Vektor im Gauß-Newton-Iterationsschritt hat die Form ${\displaystyle d=-DJ^{T}f(x)}$, wobei ${\displaystyle D=\left(J^{T}J\right)^{-1}}$. Wenn ${\displaystyle J}$ vollen Rang hat, so ist ${\displaystyle J^{T}J}$ und damit auch ${\displaystyle D}$ positiv definit. Andererseits ist ${\displaystyle J^{T}f(x)}$ der Gradient des quadratischen Problems ${\displaystyle \min _{x\in \mathbb {R} ^{n}}{\frac {1}{2}}\|f(x)\|^{2}}$, somit ist ${\displaystyle d}$ eine Abstiegsrichtung, d. h., es gilt ${\displaystyle \left(J^{T}f(x)\right)^{T}d<0}$. Daraus folgt (bei geeigneter Wahl der Schrittweite ${\displaystyle \alpha ^{k}}$) die Konvergenz der Gauß-Newton-Methode zu einem stationären Punkt. Aus dieser Darstellung lässt sich auch erkennen, dass die Gauß-Newton Methode im Wesentlichen ein skaliertes Gradientenverfahren mit der positiv definiten Skalierungsmatrix ${\displaystyle D}$ ist.

Über die Konvergenzgeschwindigkeit kann im Allgemeinen keine Aussage getroffen werden. Falls der Startpunkt ${\displaystyle x^{0}}$ sehr weit vom Optimum entfernt ist oder die Matrix ${\displaystyle J^{T}J}$ schlecht konditioniert ist, so konvergiert die Gauß-Newton-Methode u. U. nur sublinear. In vielen praktischen Anwendungsfällen konvergiert die Gauß-Newton-Methode jedoch wesentlich schneller und kann in manchen Fällen sogar dieselbe quadratische Konvergenz wie die Newton-Methode erreichen. Dies ist aus der Verwandtschaft zur Newton-Methode ersichtlich: Die Taylorentwicklung 2. Ordnung der Zielfunktion lautet

${\displaystyle {\tilde {f}}(x)\approx f(x^{0})+\nabla f(x^{0})^{T}(x-x^{0})+{\frac {1}{2}}(x-x^{0})^{T}H(x^{0})(x-x^{0})}$

wobei ${\displaystyle H(x^{0})}$ die Hesse-Matrix im Punkt ${\displaystyle x^{0}}$ ist. Für den Fall, dass ${\displaystyle H(x)}$ klein ist (z. B. wenn ${\displaystyle f(x)}$ fast linear ist, oder wenn die Komponentenfunktionen ${\displaystyle f_{i}(x)}$ in der Nähe des Optimums sehr klein sind), kann der quadratische Term vernachlässigt werden und die Gauß-Newton-Methode konvergiert superlinear. Gilt im optimalen Punkt ${\displaystyle x^{*}}$ dass ${\displaystyle H(x^{*})=0}$, dann ist der entsprechende Newton-Schritt identisch mit dem Gauss-Newton-Schritt und die Konvergenz der Gauß-Newton-Methode ist quadratisch.

Erweiterung

Um das Verhalten im Fall von schlecht konditionierten bzw. singulären ${\displaystyle J^{T}J}$ zu verbessern, kann der Gauß-Newton-Iterationsschritt folgendermaßen modifiziert werden

${\displaystyle x^{k+1}=x^{k}-\alpha ^{k}\left((J|_{x^{k}})^{T}J|_{x^{k}}+\Delta ^{k}\right)^{-1}(J|_{x^{k}})^{T}f(x^{k})}$,

wobei die Diagonalmatrix ${\displaystyle \Delta ^{k}}$ so gewählt wird, dass ${\displaystyle J|_{x^{k}}^{T}J|_{x^{k}}+\Delta ^{k}}$ positiv definit ist. Mit der Wahl ${\displaystyle \Delta ^{k}=\beta ^{k}I,\ \beta \geq 0}$, also einem skalaren Vielfachen der Identitätsmatrix, erhält man den Levenberg-Marquardt-Algorithmus.

Beispiel

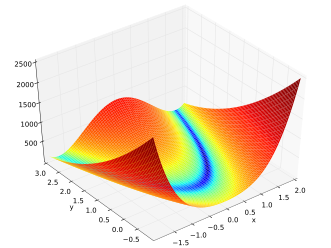
Die Rosenbrock-Funktion

${\displaystyle g:\mathbb {R} ^{2}\to \mathbb {R} :x\mapsto \left(a-x_{1}\right)^{2}+b\left(x_{2}-x_{1}^{2}\right)^{2}}$

wird häufig als Test für Optimierungsmethoden verwendet, da sie wegen des schmalen und flachen Tals, in welchem iterative Methoden nur kleine Schritte machen können, eine Herausforderung darstellt. Die Konstanten werden üblicherweise mit ${\displaystyle a=1,\ b=100}$ gewählt, das globale Optimum liegt in diesem Fall bei ${\displaystyle x^{*}=(1,1)}$ mit dem Funktionswert ${\displaystyle g(x^{*})=0}$.

Um die Gauß-Newton-Methode anzuwenden, muss die Rosenbrock-Funktion zunächst in die Form "Summe von Quadraten von Funktionen" gebracht werden. Da die Rosenbrock-Funktion bereits aus einer Summe von zwei Termen besteht, wählt man den Ansatz

${\displaystyle {\frac {1}{2}}\left(f_{1}(x)\right)^{2}=\left(a-x_{1}\right)^{2}\ \ \Longleftrightarrow \ \ f_{1}(x)={\sqrt {2}}(a-x_{1})}$

und

${\displaystyle {\frac {1}{2}}\left(f_{2}(x)\right)^{2}=b\left(x_{2}-x_{1}^{2}\right)^{2}\ \ \Longleftrightarrow \ \ f_{2}(x)={\sqrt {2b}}(x_{2}-x_{1}^{2})}$.

Das Gauß-Newton-Problem für die Rosenbrock-Funktion lautet somit

${\displaystyle \min _{x\in \mathbb {R} ^{2}}{\frac {1}{2}}\|f(x)\|^{2}}$ wobei ${\displaystyle f:\mathbb {R} ^{2}\to \mathbb {R} ^{2}:x\mapsto {\begin{pmatrix}f_{1}(x)\\f_{2}(x)\end{pmatrix}}={\begin{pmatrix}{\sqrt {2}}(a-x_{1})\\{\sqrt {2b}}(x_{2}-x_{1}^{2})\end{pmatrix}}}$.

Die Jacobi-Matrix ergibt sich als ${\displaystyle J={\begin{bmatrix}{\tfrac {\partial f_{1}}{\partial x_{1}}}&{\tfrac {\partial f_{1}}{\partial x_{2}}}\\{\tfrac {\partial f_{2}}{\partial x_{1}}}&{\tfrac {\partial f_{2}}{\partial x_{2}}}\end{bmatrix}}={\begin{bmatrix}-{\sqrt {2}}&0\\-2x_{1}{\sqrt {2b}}&{\sqrt {2b}}\end{bmatrix}}}$ und damit ist ${\displaystyle D=J^{T}J={\begin{bmatrix}8bx_{1}^{2}+2&-4bx_{1}\\-4bx_{1}&2b\end{bmatrix}}}$. Da ${\displaystyle J}$ vollen Rang hat, ist ${\displaystyle D}$ positiv definit und die Inverse ${\displaystyle D^{-1}}$existiert. Zur Bestimmung der Schrittweite ${\displaystyle \alpha ^{k}}$ kommt folgende einfache Liniensuche zum Einsatz:

1. Starte mit ${\displaystyle \alpha ^{k}=1}$.
2. Berechne den neuen Punkt ${\displaystyle {\tilde {x}}=x^{k}+\alpha ^{k}d}$ mit ${\displaystyle d=-\left((J|_{x^{k}})^{T}J|_{x^{k}}\right)^{-1}(J|_{x^{k}})^{T}f(x^{k})}$.
3. Wenn ${\displaystyle g({\tilde {x}})<g(x^{k})}$ setze ${\displaystyle x^{k+1}={\tilde {x}}}$ und gehe zur nächsten Iteration.
4. Ansonsten halbiere ${\displaystyle \alpha ^{k}}$ und gehe zu 2.

Die Liniensuche erzwingt, dass der neue Funktionswert kleiner als der vorherige ist; sie terminiert garantiert (mit ev. sehr kleinem ${\displaystyle \alpha ^{k}}$), da ${\displaystyle d}$ eine Abstiegsrichtung ist.

Als Startpunkt wird ${\displaystyle x^{0}=(0,-0.1)}$ gewählt. Die Gauß-Newton-Methode konvergiert in wenigen Iterationen zum globalen Optimum:

Optimierung mit Gauß-Newton Methode

${\displaystyle k}$	${\displaystyle x^{k}}$	${\displaystyle g(x^{k})}$
0	(0, -0.1)	2
1	(0.1250, -0.0875)	1.8291
2	(0.2344, -0.0473)	1.6306
3	(0.4258, 0.0680)	1.6131
4	(0.5693, 0.2186)	1.3000
5	(0.7847, 0.5166)	1.0300
6	(1.0, 0.9536)	0.2150
7	(1.0, 1.0)	1.1212e-27

Das Gradientenverfahren (mit derselben Liniensuche) liefert im Vergleich dazu folgendes Ergebnis, es findet selbst nach 500 Iterationen nicht zum Optimum:

Optimierung mit Gradientenverfahren

${\displaystyle k}$	${\displaystyle x^{k}}$	${\displaystyle g(x^{k})}$
0	(0, -0.1)	2
1	(0.0156, 0.0562)	1.2827
2	(0.0337, -0.0313)	1.0386
3	(0.0454, 0.0194)	0.9411
4	(0.0628, -0.0077)	0.8918
5	(0.0875, 0.0286)	0.8765
${\displaystyle \vdots }$	${\displaystyle \vdots }$	${\displaystyle \vdots }$
500	(0.8513, 0.7233)	0.0223

Literatur

• Dimitri P. Bertsekas: Nonlinear Programming. Second Edition, Athena Scientific, 1995, ISBN 978-1-886529-14-4.
• Yurii Nesterov: Introductory Lectures on Convex Optimization: A Basic Course. Springer Science & Business Media, 2003, ISBN 978-1-4419-8853-9.
• Jorge Nocedal, Stephen Wright: Numerical Optimization. Springer Science & Business Media, 2000, ISBN 978-0-387-98793-4.
• Amir Beck: Introduction to Nonlinear Optimization. SIAM, 2014, ISBN 978-1-61197-364-8.

Einzelnachweise

1. ↑ Ceres Solver Dokumentation. Abgerufen am 10. Mai 2019.