Assoziativgesetz

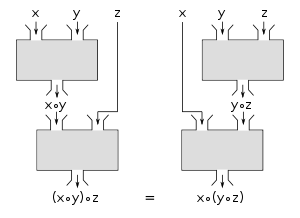
Das Assoziativgesetz, genauer die Assoziativität (lateinisch associare „vereinigen, verbinden, verknüpfen, vernetzen“), auf Deutsch Verknüpfbarkeit, ist in der Mathematik eine Eigenschaft mancher (meist zweistelligen) Verknüpfungen. Eine Verknüpfung ist assoziativ, wenn alle Reihenfolgen der Ausführung dasselbe Ergebnis haben. Anders gesagt: Die Klammerung kann bei einer assoziativen Verknüpfung beliebig gewählt werden.

Neben dem Assoziativgesetz sind Kommutativgesetz und Distributivgesetz von elementarer Bedeutung in der Algebra.

Definition

Eine binäre Verknüpfung ${\displaystyle {\star }\colon A\times A\to A}$ auf einer Menge ${\displaystyle A}$ heißt assoziativ, wenn für alle ${\displaystyle a,b,c\in A}$ das Assoziativgesetz

${\displaystyle a\star \left(b\star c\right)=\left(a\star b\right)\star c}$

gilt. Die Klammern können dann weggelassen werden. Das gilt auch für mehr als drei Operanden.

Beispiele und Gegenbeispiele

Als Verknüpfungen auf den reellen Zahlen sind Addition und Multiplikation assoziativ. So gilt zum Beispiel

${\displaystyle (2+3)+7=5+7=12\quad =}$

${\displaystyle 2+(3+7)=2+10=12}$

und

${\displaystyle (2\cdot 3)\cdot 7=6\cdot 7=42\quad =}$

${\displaystyle 2\cdot (3\cdot 7)=2\cdot 21=42}$ .

Reelle Subtraktion und Division sind hingegen nicht assoziativ, denn es ist

${\displaystyle 2-(3-1)=0\quad \neq }$

${\displaystyle (2-3)-1=-2}$

und

${\displaystyle (4:2):2=1\quad \neq }$

${\displaystyle 4:(2:2)=4}$ .

Auch die Potenz ist nicht assoziativ, da

${\displaystyle 2^{(2^{3})}=2^{8}=256\quad \neq }$

${\displaystyle (2^{2})^{3}=4^{3}=64}$

gilt. Bei (divergenten) unendlichen Summen kann es auf die Klammersetzung ankommen. So verliert die Addition die Assoziativität bei:

${\displaystyle (1+(-1))+(1+(-1))+(1+(-1))+(1+(-1))+\ldots =0+0+\ldots \to 0}$

aber

${\displaystyle 1+((-1)+1)+((-1)+1)+((-1)+1)+\ldots =1+0+0+\ldots \to 1}$

In endlichen Realisierungen wie dem Computer sind die Darstellungen der Zahlen in ihrer Größe begrenzt. Somit können weder Addition noch Multiplikation beliebig korrekt sein. Addition und Multiplikation von Festkommazahlen kann man bei vielen Maschinen so einstellen, dass diese anzeigen, wenn das Ergebnis inkorrekt wird, und innerhalb eines so definierten Gültigkeitsbereiches sind die Operationen assoziativ. Außerhalb dieses Gültigkeitsbereiches können die Operationen zwar assoziativ sein, was aber angesichts des falschen Ergebnisses keine Bedeutung hat. Bei Gleitkommazahlen werden nicht alle sog. Rundungsfehler angezeigt, so dass die Assoziativgesetze nicht wirklich gelten, wie das folgende Beispiel für die Addition mit 4-Bit-Mantissen zeigt:

(1.000₂×2⁰ + 1.000₂×2⁰) + 1.000₂×2⁴ = 1.000₂×2¹ + 1.000₂×2⁴ = 1.001₂×2⁴

1.000₂×2⁰ + (1.000₂×2⁰ + 1.000₂×2⁴) = 1.000₂×2⁰ + 1.000₂×2⁴ = 1.000₂×2⁴

Solche Fehler können manchmal durch Ausschalten der Normalisierung verringert werden.
Darüber hinaus kann das Laufzeitverhalten von der Reihenfolge der Ausführung zweier Operationen stark abhängen.

Einordnung

Das Assoziativgesetz gehört zu den Gruppenaxiomen, wird aber bereits für die schwächere Struktur einer Halbgruppe gefordert.

Seitigkeit

Insbesondere bei nicht-assoziativen Verknüpfungen gibt es Konventionen einer seitigen Assoziativität.

Eine binäre Verknüpfung ${\displaystyle *}$ gilt als links-assoziativ, wenn

${\displaystyle {\begin{array}{ll}a*b*c&:=(a*b)*c\qquad \qquad \quad \,\\a*b*c*d&:=((a*b)*c)*d\quad \\{\mbox{etc.}}\end{array}}}$

aufzufassen ist.

• Die nicht-assoziativen Operationen Subtraktion und Division werden gemeinhin links-assoziativ verstanden:^[1][2][3]

	${\displaystyle a-b-c}$	${\displaystyle =(a-b)-c}$	(Subtraktion)
	${\displaystyle a:b:c}$	${\displaystyle =(a:b):c}$	(Division)

• Anwendung von Funktionen
  ${\displaystyle (f\,x\,y)=((f\,x)\,y)}$
  im Verfahren des Currying.

Eine binäre Verknüpfung ${\displaystyle *}$ heißt rechts-assoziativ, wenn gilt:

${\displaystyle {\begin{array}{rr}x*y*z:=&x*(y*z)\\w*x*y*z:=&w*(x*(y*z))\\&{\mbox{etc.}}\end{array}}}$

Beispiel für eine rechts-assoziative Operation:

• Exponenzieren reeller Zahlen in Exponentenschreibweise:

${\displaystyle x^{y^{z}}=x^{(y^{z})}}$

Aber auch assoziative Operationen können Seitigkeit haben, wenn sie ins Unendliche zu iterieren sind.

• Die dezimale Notation rechts vom Dezimalkomma
  ${\displaystyle 0{,}999\ldots =0{,}9999\ldots =0{,}99999\ldots \to 1}$
  ist eine links-assoziative Verkettung der Dezimalziffern, weil die Auswertung(sschleife) nicht rechts bei den Auslassungspunkten ${\displaystyle \ldots }$ beginnen kann, sondern links beginnen muss.
• Die ${\displaystyle p}$-adische Schreibweise
  ${\displaystyle \ldots 444_{5}=\ldots 4444_{5}=\ldots 44444_{5}\to -1}$
  enthält mit der Juxtaposition eine rechts-assoziative Verkettungsoperation, weil die Auswertung rechts beginnen muss.

Schwächere Formen des Assoziativgesetzes

Folgende Abschwächungen des Assoziativgesetzes werden an anderer Stelle genannt/definiert:

• Potenz-Assoziativität:
  ${\displaystyle a^{r+s}=(a^{r})\circ (a^{s})}$
  • i-Potenz-Assoziativität:
    ${\displaystyle a^{i}\circ a=a\circ a^{i}}$
  • Idemassoziativität:
    ${\displaystyle a\circ (a\circ a)=(a\circ a)\circ a}$
• Alternativität:
  • Linksalternativität:
    ${\displaystyle a\circ (a\circ b)=(a\circ a)\circ b}$
  • Rechtsalternativität:
    ${\displaystyle a\circ (b\circ b)=(a\circ b)\circ b}$
• Flexibilitätsgesetz:
  ${\displaystyle a\circ \left(b\circ a\right)=\left(a\circ b\right)\circ a}$
• Moufang-Identitäten:
  ${\displaystyle {\Big (}a\circ (b\circ a){\Big )}\circ c=a\circ {\Big (}b\circ (a\circ c){\Big )}}$
  ${\displaystyle (a\circ b)\circ (c\circ a)=a\circ {\Big (}(b\circ c)\circ a{\Big )}}$
• Bol-Identitäten:^[4]
  • linke Bol-Identität:
    ${\displaystyle {\Big (}b\circ (c\circ b){\Big )}\circ a=b\circ {\Big (}c\circ (b\circ a){\Big )}}$
  • rechte Bol-Identität:
    ${\displaystyle {\Big (}(a\circ b)\circ c{\Big )}\circ b=a\circ {\Big (}(b\circ c)\circ b{\Big )}}$
• Jordan-Identität:
  ${\displaystyle a\circ {\Big (}\left(a\circ a\right)\circ b{\Big )}=\left(a\circ a\right)\circ \left(a\circ b\right)}$

Siehe auch

• Algebra
• Operatorassoziativität

Literatur

• Otto Forster: Analysis 1: Differential- und Integralrechnung einer Veränderlichen. Vieweg-Verlag, München 2008, ISBN 978-3-8348-0395-5. 

Einzelnachweise

1. ↑ Bronstein: Taschenbuch der Mathematik. Kapitel: 2.4.1.1, ISBN 978-3-8085-5673-3, S. 115–120
2. ↑ George Mark Bergman: Order of arithmetic operations
3. ↑ The Order of Operations. Education Place
4. ↑ Gerrit Bol: Gewebe und Gruppen In: Mathematische Annalen, 114 (1), 1937, S. 414–431.