Anàlisi harmònica

L'anàlisi harmònica o anàlisi de Fourier o anàlisi harmònica de Fourier^[1] és la branca de les matemàtiques que estudia la representació de les funcions o dels senyals com a superposició d'ones de base. Estudia la representació de funcions periòdiques en base a la suma i la integració de desenvolupaments en sèrie de funcions trigonomètriques elementals.^[2][1] Aprofundeix i generalitza les nocions de sèrie de Fourier i de transformada de Fourier. Les ones de base es diuen les harmòniques, d'on pren el nom de la disciplina. Durant aquests dos últims segles, ha tingut nombroses aplicacions en física sota el nom d'anàlisi espectral, i s'han obtingut aplicacions recents sobretot en tractament del senyal, mecànica quàntica, neurociències, estratigrafia…

L'anàlisi harmònica, que històricament havia estat vinculada al desenvolupament de la teoria de les sèries de Fourier, ha rebut un conjunt de generalitzacions modernes, sobretot gràcies als treballs de l'escola russa de Guelfand, que la situa en un context molt general i abstracte: per exemple, l'anàlisi harmònica sobre els grups de Lie.

Etimologia

El terme «harmònics» es va originar de la paraula en grec antic harmonikos, que significa «hàbil en música».^[3] En problemes físics de valor propi, va començar a significar ones les freqüències de les quals són múltiples enters entre si, com ho són. les freqüències de la harmònics de notes musicals. Tot i així, el terme s'ha generalitzat més enllà del seu significat original.

Sèries i transformades de Fourier

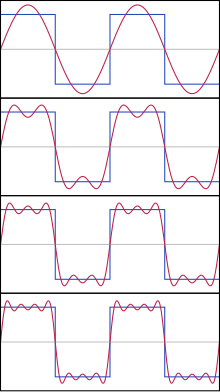
Les sèries de Fourier es fan servir per a descompondre una funció periòdica f com una «suma infinita de funcions trigonomètriques» de freqüències múltiples d'una freqüència fonamental. Al principi, es procedeix a l'anàlisi del «contingut en freqüències», anomenat espectre, de la funció. Després, seguint les hipòtesis fetes sobre la funció i el marc d'anàlisi escollit, es poden fer servir diversos teoremes que permeten recompondre f.^[4]

Un bon marc d'estudi per a les sèries de Fourier és el dels espais de Hilbert, el qual subministra a una relació entre anàlisi harmònica i anàlisi funcional.

La transformada de Fourier generalitza la teoria de les sèries de Fourier a les funcions no periòdiques, i permet associar-les també un espectre de freqüències. Llavors s'intenta descompondre una funció qualsevol en «suma infinita de funcions trigonomètriques» de totes les freqüències. Aquesta mena de sumatori es presentarà doncs en forma d'integral.

La transformada de Fourier clàssica sobre Rⁿ és encara un àmbit de recerca actiu, en particular la transformació de Fourier sobre objectes més generals com les distribucions. Per exemple, si s'imposen restriccions a una distribució f, es poden traduir sobre la seva transformada de Fourier. El teorema de Paley-Wiener n'és un exemple. Aquest teorema té com a conseqüència immediata que si f és una distribució no nul·la amb suport compacte, llavors la seva transformada de Fourier no és mai amb suport compacte. És una forma elemental de les relacions d'incertesa de Heisenberg.

Anàlisi harmònica abstracta

Una de les branques més modernes de l'anàlisi harmònica, iniciada a mitjans del segle xx, és l'anàlisi sobre els grups topològics. La idea és que la transformació de Fourier es pot generalitzar en una transformació de les funcions definides sobre grups localment compactes.

La teoria per als grups abelians localment compactes és la dualitat de Pontryagin. L'anàlisi harmònica estudia les propietats d'aquesta dualitat i intenta estendre-les a altres estructures, per exemple els grups de Lie no abelians. En general, per als grups no abelians localment compactes, l'anàlisi harmònica està vinculada a la teoria de les representacions dels grups unitaris. Per als grups compactes, el teorema de Peter-Weyl explica com obtenir els harmònics escollint una representació irreductible en cada classe d'equivalència. Aquesta tria dels harmònics permet aprofitar certes propietats útils de la transformació de Fourier que transforma el producte de convolució en producte usual i revela l'estructura de grup subjacent.

Si el grup no és ni abelià ni compacte, fins al present no es coneix cap teoria satisfactòria, és a dir equivalent almenys al teorema de Plancherel. Però particulars s'han estudiat certs casos particulars, com per exemple el grup especial lineal SL_n. En aquest cas, les representacions de dimensió infinita tenen un paper crucial.

Altres branques

• Estudi dels valor propis i vectors propis del Laplacià en dominis, varietats i (a un menor extent) grafs també es considera una branca de l'anàlisi harmònica. Vegeu, per exemple, escoltar la forma d'un tambor.^[5]
• L'anàlisi harmònic d'espais euclidians tracta de propietats de la transformada de Fourier a Rⁿ que no tenen anàleg en grups generals. Per exemple, el fet que la transformada de Fourier sigui invariant de rotació. La descomposició de la transformada de Fourier en els seus components radial i esfèric condueix a temes com ara funció de Bessels i harmònics esfèrics.
• L'anàlisi harmònic en dominis de tubs s'ocupa de generalitzar les propietats dels espais Hardy a dimensions superiors.

Referències

Bibliografia

Aquest article té bibliografia, però no se sap quina referència verifica cada part. Podeu millorar aquest article assignant cadascuna d'aquestes obres a frases o paràgrafs concrets.

• Gasquet, Claude; Witomski, Patrick. Analyse de Fourier et applications: filtrage, calcul numérique, ondelettes (en francès). Dunod, 2000. ISBN 2-10-005018-X. 
• Gasquet, Claude; Witomski, Patrick. Analyse de Fourier et applications: filtrage, calcul numérique, ondelettes (en francès). Paris Milan Barcelone: Masson, 2004. ISBN 2-225-82018-X. 
• Stein, Elias M.; Murphy, Timothy S.. Harmonic analysis: real-variable methods, orthogonality, and oscillatory integrals (en anglès). Princeton, N.J: Princeton University Press, 1993. ISBN 0-691-03216-5. 
• Wolff, Thomas H.; Łaba, Izabella; Shubin, Carol. Lectures on harmonic analysis (en anglès). Providence (R.I.): American mathematical society, 2003. ISBN 0-8218-3449-5. 
• Katznelson, Yitzhak. An introduction to harmonic analysis (en anglès). 3rd. Cambridge New York: Cambridge university press, 2004. ISBN 0-521-83829-0. 
• Terras, Audrey. Harmonic Analysis on Symmetric Spaces-Euclidean Space, the Sphere, and the Poincaré Upper Half-Plane (en anglès). 2a. Nova York: Springer, 2013. ISBN 978-1461479710. 

Enllaços externs

• Anàlisi de Fourier Arxivat 2010-06-19 a Wayback Machine., curs de J. Fàbrega a la Universitat Politècnica de Catalunya.(català)
• Introduction à l'analyse de Fourier Arxivat 2008-09-14 a Wayback Machine., curs en el lloc web del Laboratori de tractament del senyal de l'Escola politècnica federal de Lausanne (francès)
• Harmonic Analysis, definició al lloc web MathWorld (anglès)